Пределы функций
Для
определения пределов последовательностей и функций используются некоторые
известные приемы:
1. Если необходимо найти предел
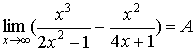 , ,
можно
предварительно привести к общему знаменателю
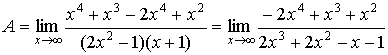 . .
Поделив на член, имеющий максимальную степень, получим в
числителе постоянную величину, а в знаменателе – все члены, стремящиеся к 0,то
есть
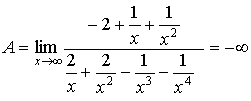 . .
2. Аналогично, для примера 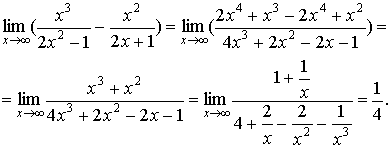
3. 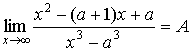 в этом пределе, если подставить x=a, то
получится неопределенность, которую можно преодолеть, если разложить разность
кубов в знаменателе в этом пределе, если подставить x=a, то
получится неопределенность, которую можно преодолеть, если разложить разность
кубов в знаменателе 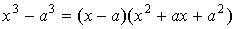 , а числитель в виде: , а числитель в виде: 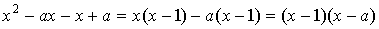 . .
Тогда
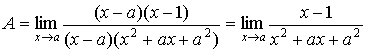 и подставив x=a,
получим: и подставив x=a,
получим: 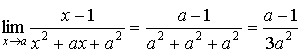 ; ;
4. 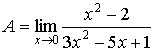 ,
при подстановке х=0, получим ,
при подстановке х=0, получим 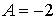 . .
5. Однако,
если необходимо найти предел рациональной функции
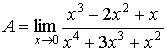 , то при делении на член с минимальной степенью, получим , то при делении на член с минимальной степенью, получим
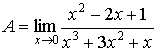 ; и, устремив х к 0, получим: ; и, устремив х к 0, получим: 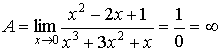
Если в пределах содержатся иррациональные выражения, то
приходится вводить новые переменные для получения рационального выражения, или
же переводить иррациональности из знаменателя в числитель и наоборот.
6. 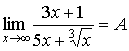 ; Сделаем замену
переменной. Заменим ; Сделаем замену
переменной. Заменим 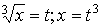 , при , при 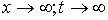 , получим , получим 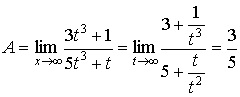 . .
7. 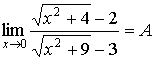 . Если числитель и знаменатель умножить на одно и то же
число, то предел не изменится. Умножим числитель на . Если числитель и знаменатель умножить на одно и то же
число, то предел не изменится. Умножим числитель на 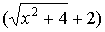 и разделим на это же
выражение, чтобы предел не изменился, а знаменатель умножим на и разделим на это же
выражение, чтобы предел не изменился, а знаменатель умножим на 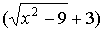 и разделим, на это же
выражение. Тогда получим: и разделим, на это же
выражение. Тогда получим:
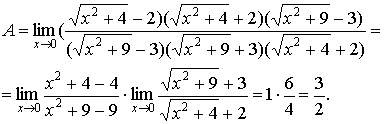
Для определения пределов часто используются
замечательные пределы:
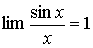 ; (1) ; (1)
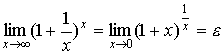 . (2) . (2)
8. 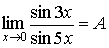 . .
Для вычисления такого предела сведем его к 1-му
замечательному пределу (1). Для этого умножим и разделим числитель на 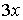 , а знаменатель на , а знаменатель на 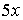 , тогда , тогда 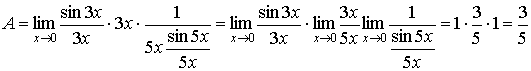 . .
9. 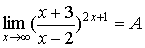 Для вычисления этого
предела сведем его ко второму замечательному пределу. С этой целью из
рационального выражения в скобках выделим целую часть и представим ее в виде
правильной дроби. Так поступают в тех случаях, когда Для вычисления этого
предела сведем его ко второму замечательному пределу. С этой целью из
рационального выражения в скобках выделим целую часть и представим ее в виде
правильной дроби. Так поступают в тех случаях, когда 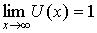 , где , где 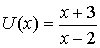 , а , а 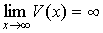 , где , где 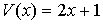 ; ;
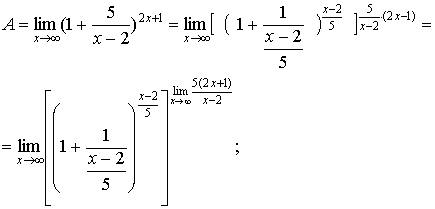
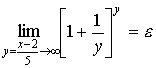 , а , а 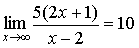 , то окончательно , то окончательно 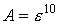 . Здесь использовалась непрерывность композиции непрерывных
функций. . Здесь использовалась непрерывность композиции непрерывных
функций.
Вычисление пределов с помощью правила Лопиталя
Все
вышеперечисленные пределы не использовали аппарат дифференциального исчисления.
Однако, если необходимо найти
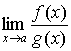 и при и при 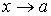 обе эти функции
бесконечно малые или обе бесконечно большие, то их отношение не определено в
точке обе эти функции
бесконечно малые или обе бесконечно большие, то их отношение не определено в
точке 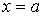 и, следовательно,
представляет собой неопределенность типа и, следовательно,
представляет собой неопределенность типа 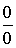 или или 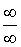 соответственно.
Поскольку это отношение в точке соответственно.
Поскольку это отношение в точке 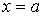 может иметь предел,
конечный или бесконечный, то нахождение этого предела называется раскрытием
неопределенности (правило Лопиталя Бернули), может иметь предел,
конечный или бесконечный, то нахождение этого предела называется раскрытием
неопределенности (правило Лопиталя Бернули),
и
имеет место следующее равенство:
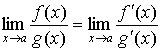 , если , если 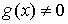 и и 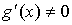 . .
1. 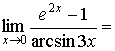 (здесь имеет место неопределенность типа (здесь имеет место неопределенность типа 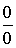 )= )=
=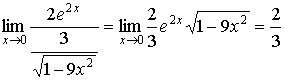 . .
Аналогичное правило имеет место, если 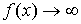 и и 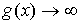 , т.е. , т.е. 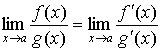 . .
2. 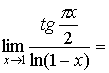 (неопределенность типа (неопределенность типа 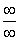 ) )
=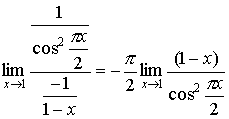
=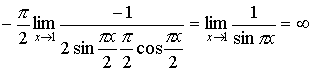 . .
Правило
Лопиталя позволяет также раскрывать неопределенности типа 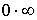 и и 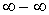 . Для вычисления . Для вычисления 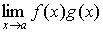 , где , где 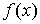 - бесконечно малая, а - бесконечно малая, а 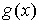 - бесконечно большая при - бесконечно большая при 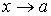 (раскрытие неопределенности типа (раскрытие неопределенности типа 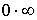 ) следует преобразовать произведение к виду ) следует преобразовать произведение к виду
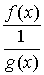 (неопределенность типа (неопределенность типа
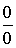 ) или к виду ) или к виду 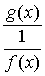 (неопределенность типа (неопределенность типа 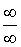 ) и далее использовать правило Лапиталя. ) и далее использовать правило Лапиталя.
3.
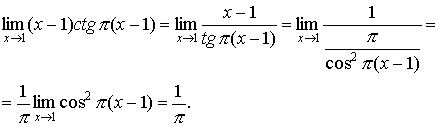
Для
вычисления 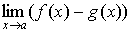 , где , где 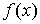 и и 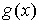 - бесконечно большие при - бесконечно большие при 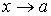 (раскрытие
неопределенности типа (раскрытие
неопределенности типа 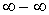 ) следует преобразовать разность к виду ) следует преобразовать разность к виду 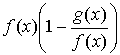 , затем раскрыть неопределенность , затем раскрыть неопределенность 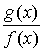 типа типа 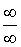 . Если . Если 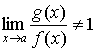 , то , то 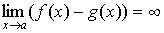 . .
Если же 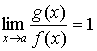 , то получается неопределенность типа ( , то получается неопределенность типа (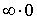 ), которая раскрывается аналогично примеру 12). ), которая раскрывается аналогично примеру 12).
4. 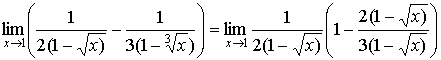 . .
Так
как 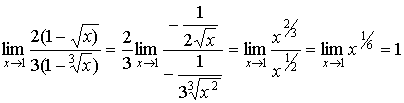 , то получим в итоге неопределенность типа , то получим в итоге неопределенность типа 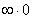 и далее имеем и далее имеем
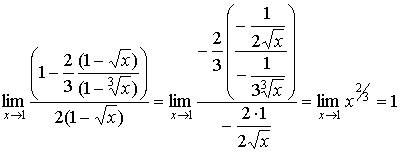 . .
Правилом Лопиталя можно
пользоваться также для раскрытия неопределенностей типа 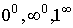 . В этих случаях имеется в виду вычисление предела выражения . В этих случаях имеется в виду вычисление предела выражения 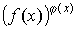 , где , где 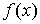 в случае в случае 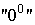 есть бесконечно малая, в случае есть бесконечно малая, в случае 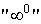 - бесконечно большая, а в случае - бесконечно большая, а в случае 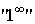 - функция, предел которой равен единице. - функция, предел которой равен единице.
Функция 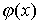 в первых двух случаях является бесконечно малой, а в
последнем случае – бесконечно большой функцией. в первых двух случаях является бесконечно малой, а в
последнем случае – бесконечно большой функцией.
Прежде
чем искать предел таких выражений, их логарифмируют, т.е. если 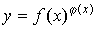 , то , то 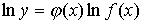 , затем находят предел , затем находят предел 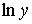 , и после чего находят предел , и после чего находят предел 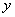 . Во всех перечисленных случаях . Во всех перечисленных случаях 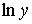 является
неопределенностью типа является
неопределенностью типа 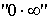 , которую раскрывают аналогично примеру 12). , которую раскрывают аналогично примеру 12).
5. 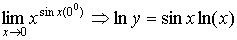
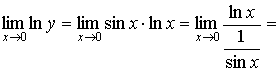 (воспользуемся правилом Лопиталя)= (воспользуемся правилом Лопиталя)=
=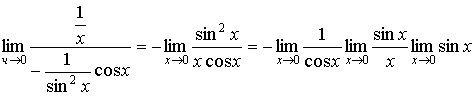 . .
В этом
произведении пределов первый равен 1, второй сомножитель представляет собой
первый замечательный предел и он тоже равен 1, а последний сомножитель
стремится к 0, следовательно:
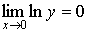 и тогда и тогда 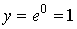 . .
6. 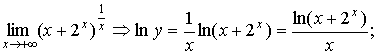
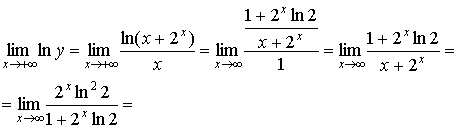 = =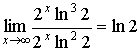 ; ;
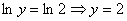 . .
7. 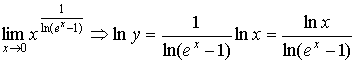 ; ;
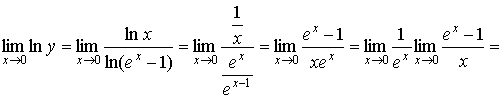
=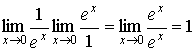 ; ;
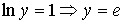 . .
8. 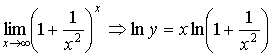 ; ;
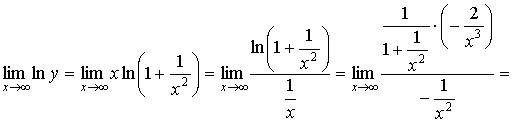
=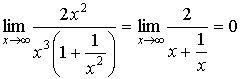 ; ;
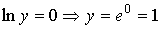 . .
|