Производная
Производной от функции 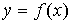 называется конечный
предел отношения приращения функции к приращению аргумента, когда последнее
стремится к нулю: называется конечный
предел отношения приращения функции к приращению аргумента, когда последнее
стремится к нулю:
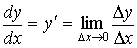 ,
или ,
или 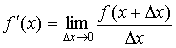 . .
Геометрически производная
представляет собой угловой коэффициент касательной к графику функции 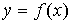 в точке х, то есть в точке х, то есть 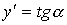 . .
Производная
есть скорость изменения функции в точке х.
Отыскание производной называется дифференцированием
функции.
Формулы
дифференцирования основных функций:
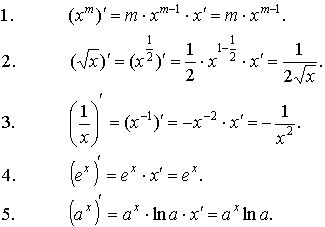
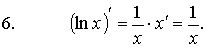
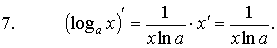
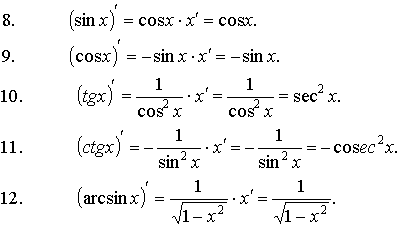
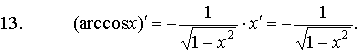
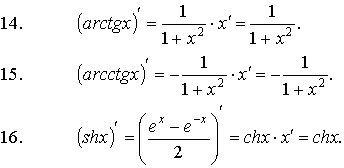
3. Основные правила дифференцирования
Пусть
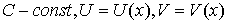 , тогда: , тогда:
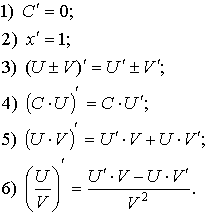
7) Если 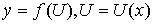 , то есть , то есть
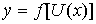 , где , где 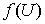 и и 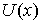 имеют производные, то имеют производные, то 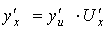 (правило
дифференцирования сложной функции). (правило
дифференцирования сложной функции).
Примеры:
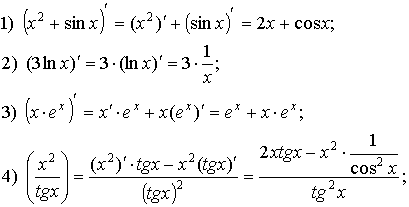
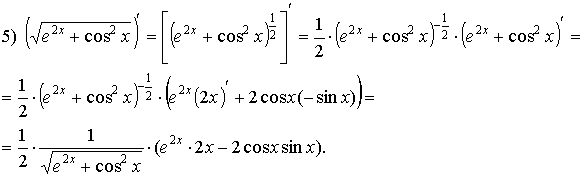
4. Логарифмическое дифференцирование
Если требуется найти 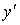 из уравнения из уравнения  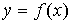 , то можно: , то можно:
а) логарифмировать обе части уравнения
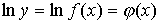 ; ;
б) дифференцировать обе части полученного равенства,
где 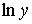 есть сложная функция от х, есть сложная функция от х,
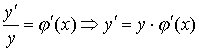 . .
в)
заменить 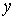 его выражением через х его выражением через х
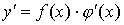 . .
Пример: 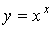
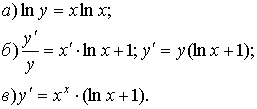
5. Дифференцирование неявных функций
Пусть уравнение 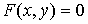 определяет определяет 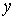 как неявную функцию от
х. как неявную функцию от
х.
а)
продифференцируем по х обе части уравнения 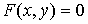 , получим уравнение первой степени относительно , получим уравнение первой степени относительно 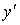 ; ;
б) из полученного уравнения выразим 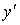 . .
Пример: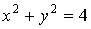 . .
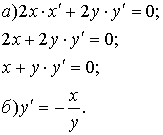
6. Дифференцирование функций, заданных параметрически
Пусть функция задана
параметрическими уравнениями 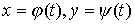 , ,
тогда
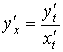 , или , или 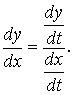
Приме: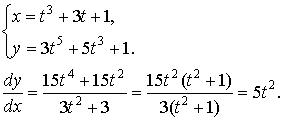
7. Приложение производной к задачам
геометрии и механики
Пусть 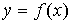 и и 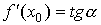 , где , где 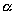 -угол, образованный с положительным направлением оси ОХ
касательной к кривой в точке с абсциссой -угол, образованный с положительным направлением оси ОХ
касательной к кривой в точке с абсциссой 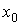 . .
Уравнение касательной к кривой 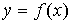 в точке в точке 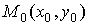 имеет вид: имеет вид:
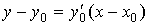 , где , где 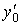 -производная -производная 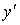 при при 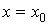 . .
Нормалью к кривой называется прямая, перпендикулярная
касательной и проходящая через точку касания.
Уравнение
нормали имеет вид
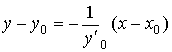 . .
Угол между двумя кривыми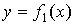 и и 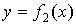 в точке их пересечения в точке их пересечения
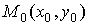 называется угол между касательными к этим кривым в точке называется угол между касательными к этим кривым в точке 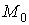 . Этот угол находится по формуле . Этот угол находится по формуле
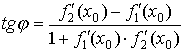 . .
8. Производные высших порядков
Если 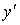 есть производная от
функции есть производная от
функции 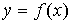 , то производная от , то производная от 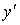 называется второй
производной, или производной второго порядка и обозначается называется второй
производной, или производной второго порядка и обозначается 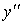 , или , или 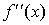 , или , или 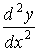 . .
Аналогично определяются производные любого
порядка:производная третьего порядка 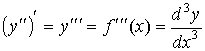 ; производная n-го порядка: ; производная n-го порядка:
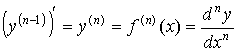 . .
Для произведения двух функций можно получить
производную любого n-го порядка, пользуясь формулой Лейбница:
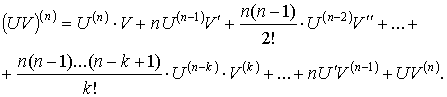
Пример:
1)
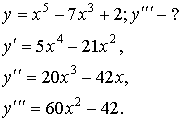
9. Вторая производная от неявной функции
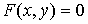 -уравнение
определяет -уравнение
определяет 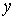 , как неявную функцию от х. , как неявную функцию от х.
а)
определим 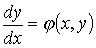 ; ;
б) продифференцируем по х левую и правую части
равенства 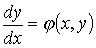 , ,
причем, дифференцируя функцию 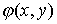 по переменной х, помним, что по переменной х, помним, что 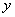 есть функция от х: есть функция от х:
 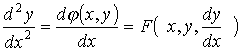 ; ;
в)
заменяя 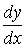 через через 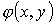 , получим: , получим: 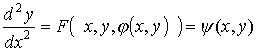 и т.д. и т.д.
Пример:
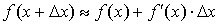
10. Производные от функций, заданных
параметрически
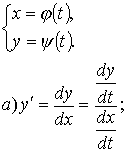
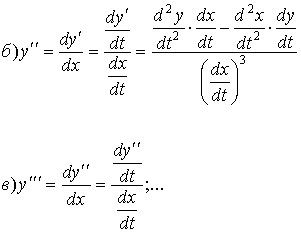
Пример:
Найти
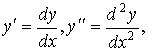 если если 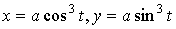 . .
11. Дифференциалы первого и высших порядков
  Дифференциалом первого порядка функции Дифференциалом первого порядка функции 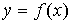 называется главная, линейная относительно аргумента часть .
Дифференциалом аргумента называется приращение аргумента: называется главная, линейная относительно аргумента часть .
Дифференциалом аргумента называется приращение аргумента: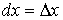 . .
Дифференциал функции равен произведению ее
производной на дифференциал аргумента:
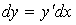 . .
Основные
свойства дифференциала:
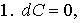 где где
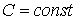 . .
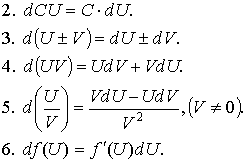
Если приращение 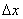 аргумента мало по абсолютной величине, то аргумента мало по абсолютной величине, то 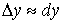 и и 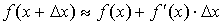 . .
Таким образом, дифференциал функции может применяться для
приближенных вычислений.
Дифференциалом
второго порядка функции 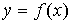 называется
дифференциал от дифференциала первого порядка: называется
дифференциал от дифференциала первого порядка: 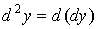 . .
Аналогично:
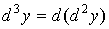 . .
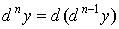 . .
Если 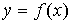 и и 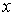 - независимая переменная, то дифференциалы высших порядков
вычисляются по формулам - независимая переменная, то дифференциалы высших порядков
вычисляются по формулам
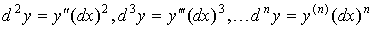 . .
Пример.
Найти дифференциалы первого и второго порядков функции
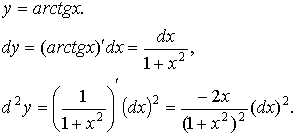
|