|
Лекция
13
Ориентированный граф и его
графическая интерпретация.Локальные степени. Матрица смежностей.
Ориентированные пути и связность в ориентированном графе.
Ориентированный
граф (или сокращенно орграф) -
это пара множеств 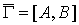 , где , где  - любое непустое
конечное множество, а - любое непустое
конечное множество, а  - подмножество в - подмножество в 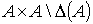 (здесь (здесь 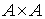 - прямое произведение
множества - прямое произведение
множества  на себя, т.е.
множество всех упорядоченных пар элементов из на себя, т.е.
множество всех упорядоченных пар элементов из  , и , и 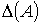 - диагональ множества - диагональ множества  ). Элементы из ). Элементы из  называются вершинами орграфа, а элементы из называются вершинами орграфа, а элементы из  - его ребрами. - его ребрами.
Если 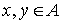 и и 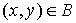 , то , то 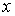 называется началом, а называется началом, а 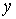 называется концом ребра называется концом ребра 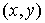 ; как и в «неориентированном случае», вершины ; как и в «неориентированном случае», вершины 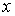 , , 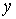 называются инцидентными ребру называются инцидентными ребру 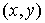 , а ребро , а ребро 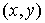 называется инцидентным вершинам называется инцидентным вершинам 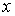 , , 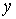 . .
Орграф имеет естественную
геометрическую интерпретацию: его вершины изображаются в виде точек на
плоскости, а ребра – в виде стрелок, идущих из начала в конец ребра. Например,
если орграф 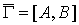 имеет в качестве
множества вершин имеет в качестве
множества вершин 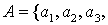 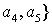 и в качестве множества
ребер и в качестве множества
ребер 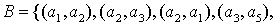 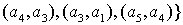 то геометрически он выглядит так: то геометрически он выглядит так:
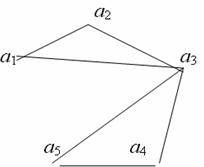
Если два орграфа
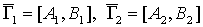 таковы, что
одновременно выполняются два условия - таковы, что
одновременно выполняются два условия - 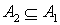 и и 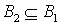 , - то говорят, что , - то говорят, что 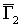 - подграф орграфа - подграф орграфа 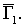 При этом пишут: При этом пишут: 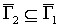 . Если одновременно . Если одновременно 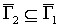 и и 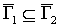 , то орграфы , то орграфы 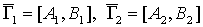 называются равными и пишут называются равными и пишут 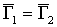 . .
Два орграфа - 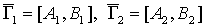 - называются изоморфными, если существует отображение - называются изоморфными, если существует отображение
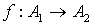 такое, что выполнены
следующие четыре условия: такое, что выполнены
следующие четыре условия:
1) если 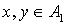 и и 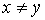 , то , то 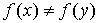 ; ;
2) для всякого 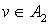 существует такой существует такой 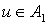 , что , что 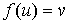 ; ;
3) если 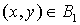 , то , то 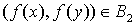 ; ;
4) если 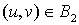 и и 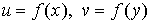 , то , то 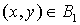 . .
Если 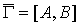 - орграф и - орграф и 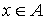 , то следующие три числа имеют специальные названия: число , то следующие три числа имеют специальные названия: число 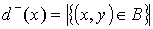 (количество ребер,
исходящих из вершины (количество ребер,
исходящих из вершины 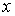 ) называется исходящей
степенью вершины ) называется исходящей
степенью вершины 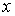 ; число ; число 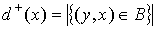 (количество ребер,
входящих в вершину (количество ребер,
входящих в вершину 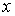 ) называется входящей
степенью вершины ) называется входящей
степенью вершины 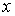 ; число ; число 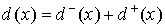 называется степенью вершины называется степенью вершины 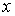 . .
Каждый орграф 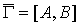 можно описать матрицей смежностей по следующей схеме:
если можно описать матрицей смежностей по следующей схеме:
если 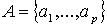 , то построим матрицу , то построим матрицу 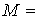 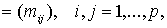 положив положив
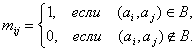
С каждым орграфом 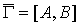 однозначно связывается
обычный граф однозначно связывается
обычный граф 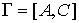 , в котором множество вершин - то же самое (т.е. множество , в котором множество вершин - то же самое (т.е. множество  ), а множество ребер ), а множество ребер 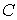 получается «стиранием
стрелок» у ребер из множества получается «стиранием
стрелок» у ребер из множества  (т.е. если (т.е. если 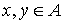 , то , то 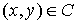 тогда и только тогда и только
тогда, когда
либо 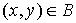 , либо , либо 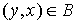 ). Граф ). Граф 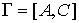 называется ассоциированным с орграфом называется ассоциированным с орграфом 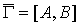 . .
В каждом орграфе 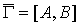 выделяется основной
объект – ориентированный путь (или
кратко - орпуть) орпуть - это символ выделяется основной
объект – ориентированный путь (или
кратко - орпуть) орпуть - это символ
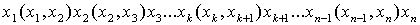 , ,
в котором 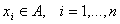 (причем, в списке (причем, в списке 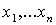 могут быть
повторяющиеся вершины) и в котором могут быть
повторяющиеся вершины) и в котором 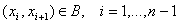 . Ясно, что при переходе от ориентированного графа к
ассоциированному с ним графу орпуть создает конкретный обычный путь. В
приведенных только что обозначениях вершина . Ясно, что при переходе от ориентированного графа к
ассоциированному с ним графу орпуть создает конкретный обычный путь. В
приведенных только что обозначениях вершина 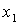 называется началом орпути, а вершина называется началом орпути, а вершина 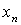 называется концом орпути. При этом о самом орпути
говорят, что он является орпутем из называется концом орпути. При этом о самом орпути
говорят, что он является орпутем из 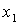 в в 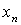 . .
Две вершины  орграфа называются связанными, если имеется орпуть из орграфа называются связанными, если имеется орпуть из  в в  и одновременно имеется
орпуть из и одновременно имеется
орпуть из  в в  . Орграф называется связным,
если в нем любые две вершины связанны. Так же, как в неориентированном случае,
понятие связности приводит к понятию
связной компоненты: подграф . Орграф называется связным,
если в нем любые две вершины связанны. Так же, как в неориентированном случае,
понятие связности приводит к понятию
связной компоненты: подграф 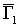 орграфа орграфа 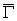 называется связной компонентой орграфа называется связной компонентой орграфа 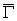 , если: 1) , если: 1) 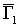 является связным
орграфом; 2) не существует связного орграфа является связным
орграфом; 2) не существует связного орграфа 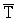 такого, что такого, что 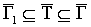 и и 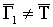 . .
Подобно тому, как это делалось в
случае обычных графов, для ориентированных графов вводятся понятия цепи,
простой цепи, цикла и простого цикла. Эти объекты можно исследовать по тому же
плану, что и в неориентированном случае.
Лекция 14
Сети
и потоки в сетях. Стационарные потоки. Алгоритм Форда-Фалкерсона поиска
максимального стационарного потока. (Данный вопрос лучше смотреть в сетевых
моделях исследования операций).
Пусть
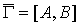 - некоторый орграф и - некоторый орграф и 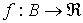 вещественно-значная
функция на множестве ребер; тогда пара вещественно-значная
функция на множестве ребер; тогда пара 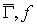 называется сетью, а функция называется сетью, а функция  в контексте сети
называется функцией пропускной
способности или пропускной способностью сети. в контексте сети
называется функцией пропускной
способности или пропускной способностью сети.
Всякая функция 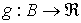 , удовлетворяющая неравенству , удовлетворяющая неравенству 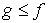 , называется потоком в
сети. В обсуждении свойств потоков в сети традиционно используется
следующее обозначение: , называется потоком в
сети. В обсуждении свойств потоков в сети традиционно используется
следующее обозначение:
пусть
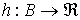 - любая функция и - любая функция и 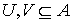 - два любых
подмножества вершин; символ - два любых
подмножества вершин; символ 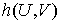 будет обозначать сумму
значений функции будет обозначать сумму
значений функции 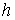 на ребрах на ребрах 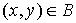 таких, что таких, что 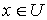 и и 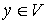 ; если ; если
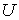 состоит из
единственной вершины состоит из
единственной вершины 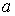 , то символ , то символ 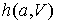 обозначает сумму весов
ребер, начинающихся в обозначает сумму весов
ребер, начинающихся в 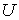 и заканчивающихся в
вершинах из и заканчивающихся в
вершинах из 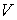 ; аналогичный смысл
имеет символ ; аналогичный смысл
имеет символ 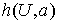 - сумма значений
функции - сумма значений
функции 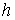 на ребрах, начинающихся
в на ребрах, начинающихся
в 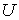 и заканчивающихся в
вершине и заканчивающихся в
вершине 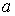 . .
Поток 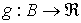 в сети в сети 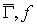 называется стационарным, если существуют две
вершины называется стационарным, если существуют две
вершины 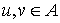 и число и число 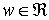 такие, что выполнены
следующие условия: такие, что выполнены
следующие условия:
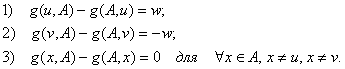
В этой ситуации
число 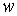 называется величиной
потока называется величиной
потока 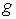 , вершина , вершина  называется источником, а вершина называется источником, а вершина  - стоком потока - стоком потока 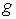 . .
Известна следующая классическая задача о максимальном потоке: в данной
сети для данного источника и для данного стока найти стационарный поток
максимально возможной величины. Можно доказать, что такая задача всегда имеет
решение. Один из способов ее ре- шения называется алгоритмом Форда-Фалкерсона. Сформулируем этот алгоритм по шагам.
Шаг 0. Фиксируем на данной
сети 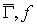 с источником с источником  и стоком и стоком  произвольный
стационарный поток произвольный
стационарный поток 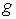 , например - поток, тождественно равный нулю (т.е. равный
нулю на каждом ребре данного орграфа , например - поток, тождественно равный нулю (т.е. равный
нулю на каждом ребре данного орграфа 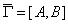 ). Нетрудно проверить, что такой поток действительно
стационарный и имеет величину 0. ). Нетрудно проверить, что такой поток действительно
стационарный и имеет величину 0.
Шаг 1. Около вершины  поставим пометку
следующего вида: поставим пометку
следующего вида:
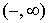 . .
Здесь символ 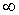 обозначает число,
заведомо превосходящее все числа, которые будут участвовать в дальнейших рассмотрениях
(в случае программирования это - компьютерная бесконечность, т.е. самое большое
число, допускаемое данным программным средством). обозначает число,
заведомо превосходящее все числа, которые будут участвовать в дальнейших рассмотрениях
(в случае программирования это - компьютерная бесконечность, т.е. самое большое
число, допускаемое данным программным средством).
Замечание.
Почти все дальнейшие действия по алгоритму представляют собой расстановку
пометок около некоторых вершин. Цель этой расстановки в том, чтобы в конце
концов поставить пометку у стока  или установить, что
сток или установить, что
сток  пометить невозможно. В
первом пометить невозможно. В
первом
случае окажется
возможным заменить имеющийся стационарный поток
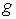 на другой стационарный
поток, имеющий величину, большую, чем величина потока на другой стационарный
поток, имеющий величину, большую, чем величина потока 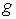 . После этого надо будет запустить все сначала. Во втором
случае окажется, что имеющийся поток . После этого надо будет запустить все сначала. Во втором
случае окажется, что имеющийся поток 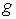 оптимален, т.е. его
величина имеет максимальное возможное значение. Каждая пометка, кроме уже
проставленной около источника оптимален, т.е. его
величина имеет максимальное возможное значение. Каждая пометка, кроме уже
проставленной около источника  , будет иметь вид , будет иметь вид 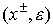 , где , где 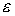 - некоторое число, а - некоторое число, а 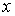 - имя одной из вер-шин
орграфа - имя одной из вер-шин
орграфа 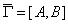 , причем реально в пометке это имя , причем реально в пометке это имя 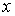 будет либо в виде будет либо в виде 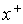 , либо в виде , либо в виде 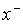 . .
Шаг 2. Пусть 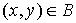 - некоторое ребро,
начало которого, т.е. вершина - некоторое ребро,
начало которого, т.е. вершина 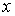 , уже имеет некоторую пометку , уже имеет некоторую пометку 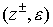 (или, если (или, если 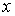 - это источник - это источник  , то пометку , то пометку 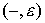 , где , где 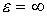 ). Ес-ли ). Ес-ли 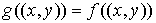 , т.е. поток , т.е. поток 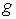 равен на ребре равен на ребре 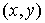 пропускной способности пропускной способности
 , то пометка у вершины , то пометка у вершины 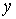 не проставляется. Если же не проставляется. Если же
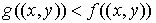 , то пометка у вершины , то пометка у вершины 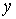 выставляется следующим
образом. выставляется следующим
образом.
На
первом месте в пометке будет стоять символ 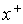 , т.е. пометка будет такой: , т.е. пометка будет такой: 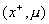 , где число , где число 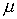 еще нужно найти. Положим еще нужно найти. Положим
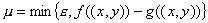 . .
Пусть теперь 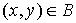 такое ребро, у
которого пометку имеет конец, т.е. вершина такое ребро, у
которого пометку имеет конец, т.е. вершина 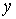 имеет пометку имеет пометку 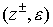 . Если . Если 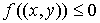 , то пометку у вершины , то пометку у вершины 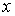 не выставляют; если же не выставляют; если же
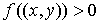 , то вершина , то вершина 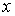 получает пометку получает пометку 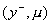 , где , где
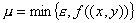 . .
Процедура расстановки пометок в
соответствии с Шагом 2 проводится до тех пор, пока не окажется
помеченной вершина 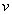 , или до тех пор, пока не выяснится, что вершину , или до тех пор, пока не выяснится, что вершину  пометить невозможно.
Можно доказать, что в последнем случае поток пометить невозможно.
Можно доказать, что в последнем случае поток 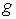 , с помощью которого проводился весь Шаг 2, имеет максимальную возможную величину, и
задача решена. , с помощью которого проводился весь Шаг 2, имеет максимальную возможную величину, и
задача решена.
Если же вершина  оказалась помеченной,
то переходим к следующему шагу. Отметим принципиальную подробность: если
вершина оказалась помеченной,
то переходим к следующему шагу. Отметим принципиальную подробность: если
вершина  оказалась помеченной,
то число, фигурирующее в пометке,
обязательно положительно. оказалась помеченной,
то число, фигурирующее в пометке,
обязательно положительно.
Шаг 3. Пусть вершина  имеет пометку имеет пометку 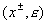 . Мы изменим сейчас поток . Мы изменим сейчас поток
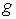 на не-скольких ребрах
данного графа, в результате чего получится новый стационарный поток из
источника на не-скольких ребрах
данного графа, в результате чего получится новый стационарный поток из
источника  в сток в сток  , величина которого будет на , величина которого будет на 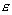 (это число указано в
пометке стока (это число указано в
пометке стока  ) больше величины потока ) больше величины потока 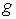 . .
Если вершина  имеет пометку имеет пометку 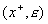 , то на ребре , то на ребре 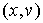 изменим поток изменим поток 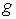 , прибавив к его значению на этом ребре число , прибавив к его значению на этом ребре число 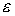 . Если вершина . Если вершина  имеет пометку имеет пометку 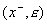 , то на ребре , то на ребре 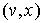 изменим поток изменим поток 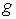 , вычитая из его значения на этом ребре число , вычитая из его значения на этом ребре число 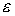 . .
Затем перейдем к вершине 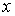 и проделаем то же, что
только что делалось относительно вершины и проделаем то же, что
только что делалось относительно вершины  ; при этом прибавлять или вычитать будем прежнее число ; при этом прибавлять или вычитать будем прежнее число 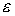 . Продолжая так, в соответствии с пометками, отбирать ребра
графа и менять на них значение потока (на каждом отбираемом ребре - на одно и
то же число . Продолжая так, в соответствии с пометками, отбирать ребра
графа и менять на них значение потока (на каждом отбираемом ребре - на одно и
то же число 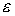 !), мы придем к источнику !), мы придем к источнику  . Это будет означать завершение изменения потока. Можно
доказать, что полученный в результате
поток является стационарным и его величина на . Это будет означать завершение изменения потока. Можно
доказать, что полученный в результате
поток является стационарным и его величина на 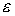 больше величины
исходного потока больше величины
исходного потока 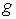 . .
Затем нужно повторить все сначала с
уже новым базовым стационарным потоком.
Пример. Найти максимальный
стационарный поток из  в в  в следующей сети
(числа у стрелок означают пропускную способность): в следующей сети
(числа у стрелок означают пропускную способность):
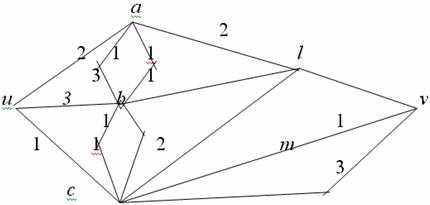
Считаем,
что исходный стационарный поток тождественно равен нулю. Проставляем пометку
около вершины  : она такова - : она такова - 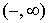 . Выбираем далее для пометки вершину . Выбираем далее для пометки вершину 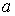 ; соответствующая пометка: ; соответствующая пометка:
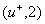 . Выбираем далее для пометки вершину . Выбираем далее для пометки вершину  ; соответствующая пометка: ; соответствующая пометка: 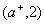 . Теперь появилась возможность пометить и вершину . Теперь появилась возможность пометить и вершину  ; соответствующая пометка : ; соответствующая пометка : 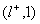 . .
Возникла возможность поток увеличить
на 1. Для этого на ребре 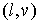 положим его равным 1
(а не нулю, как это было для исходного
потока), также равным 1 новый поток будет и на ребрах положим его равным 1
(а не нулю, как это было для исходного
потока), также равным 1 новый поток будет и на ребрах 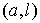 и и 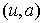 . На остальных ребрах поток остается равным нулю. . На остальных ребрах поток остается равным нулю.
Новый поток имеет величину 1, он
стационарен с источником  и стоком и стоком  . Повторим теперь процедуру сначала, стремясь поставить
пометку к стоку . Повторим теперь процедуру сначала, стремясь поставить
пометку к стоку  . .
Вершину  пометим пометкой пометим пометкой 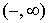 . Далее пометим вершину . Далее пометим вершину 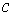 ; соответствующая пометка: ; соответствующая пометка: 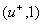 . Далее пометим вершину . Далее пометим вершину 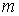 ; соответствующая пометка: ; соответствующая пометка: 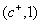 . Теперь пометим вершину . Теперь пометим вершину  ; соответствующая пометка: ; соответствующая пометка: 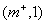 . Теперь снова увеличим на 1 значения потока на ребрах . Теперь снова увеличим на 1 значения потока на ребрах 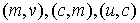 . Новый поток будет тоже стационарен, но уже величины 2. . Новый поток будет тоже стационарен, но уже величины 2.
Вновь поставим пометку 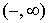 у вершины у вершины  и попытаемся увеличить
имеющийся стационарный поток величины 2. и попытаемся увеличить
имеющийся стационарный поток величины 2.
Пометим вершину 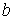 ; соответствующая пометка: ; соответствующая пометка: 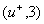 . Далее пометим вершину . Далее пометим вершину 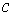 ; соответствующая пометка: ; соответствующая пометка: 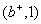 . Далее пометим вершину . Далее пометим вершину  ; соответствующая пометка: ; соответствующая пометка: 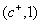 . Вновь изменим поток на 1: прибавим 1 к значениям прежнего
потока на ребрах . Вновь изменим поток на 1: прибавим 1 к значениям прежнего
потока на ребрах 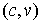 , ,
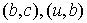 . Вновь полученный поток имеет величину 3. . Вновь полученный поток имеет величину 3.
Дальнейшие попытки достигнуть пометками
вершину  не имеют успеха.
Следовательно, максимальный стационарный поток найден. не имеют успеха.
Следовательно, максимальный стационарный поток найден.
|