|
Лекция 5
Гамильтонов
цикл и гамильтонов граф. Условия Дирака, Оре и Поша, гарантирующие
существование в графе гамильтонова цикла.
Пусть  - некоторый граф. Он
называется гамильтоновым, если в нем существует простой цикл,
содержащий все вершины графа. Например, каждый полный граф – гамильтонов,
потому что в нем проведены всевозможные ребра и, в частности, те, благодаря
которым возможен обход по всем вершинам. А вот пример графа, не являющегося
гамильтоновым: - некоторый граф. Он
называется гамильтоновым, если в нем существует простой цикл,
содержащий все вершины графа. Например, каждый полный граф – гамильтонов,
потому что в нем проведены всевозможные ребра и, в частности, те, благодаря
которым возможен обход по всем вершинам. А вот пример графа, не являющегося
гамильтоновым:
Общих и легко
осуществляемых действий, с помощью которых можно было бы достоверно выяснить,
является ли данный граф гамильтоновым, не существует. Однако, имеются
достаточные условия на гамильтоновость, которые проверяются легко. Недостаток
здесь состоит в том, что даже если ни одно из этих условий не выполняется, граф
может оказаться гамильтоновым. В дальнейшем в этой лекции будет молчаливо
предполагаться, что число вершин в любом рассматриваемом графе не меньше трех.
Итак, условие первое - условие Дирака. Пусть 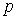 - число вершин в
данном графе; если степень каждой вершины не меньше, чем - число вершин в
данном графе; если степень каждой вершины не меньше, чем 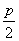 , то граф называется графом
Дирака. Можно доказать, что каждый
граф Дирака обязательно гамильтонов. , то граф называется графом
Дирака. Можно доказать, что каждый
граф Дирака обязательно гамильтонов.
Вот пример графа Дирака:
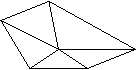
Очевидно, этот
граф - гамильтонов. А вот пример гамильтонова графа, не являющегося графом
Дирака:
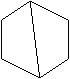
Условие второе - условие Оре. По-прежнему будем
обозначать через 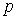 количество вер-шин в
данном графе. Если для любой пары несмежных вершин количество вер-шин в
данном графе. Если для любой пары несмежных вершин  выполнено неравенство выполнено неравенство 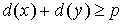 , то граф называется графом
Оре (словами: степени любых двух несмежных вершин не меньше общего числа
вершин в графе). Можно доказать, что всякий
граф Оре обязательно гамильтонов. , то граф называется графом
Оре (словами: степени любых двух несмежных вершин не меньше общего числа
вершин в графе). Можно доказать, что всякий
граф Оре обязательно гамильтонов.
Вот пример графа Оре:
А вот пример
графа, не являющегося графом Оре и, тем не менее, графа гамильтонова:

Нетрудно
заметить, что всякий граф Дирака автоматически является графом Оре. Но вот
пример графа Оре, не являющегося графом Дирака:
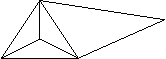
Условие третье - условие Поша. Это - более сложная
конструкция. Введем следующую функцию 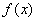 целого
неотрицательного аргумента целого
неотрицательного аргумента 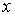 . Сначала запишем определение формулой, а затем
прокомментируем его. Итак, речь идет по-прежнему о графе . Сначала запишем определение формулой, а затем
прокомментируем его. Итак, речь идет по-прежнему о графе  , ,
для которого и
строится функция 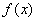 : :
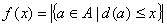 ; ;
написанное
означает, что функция 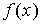 в каждом целом
неотрицательном в каждом целом
неотрицательном 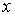 принимает значение,
равное количеству вершин графа принимает значение,
равное количеству вершин графа  , степень которых не превосходит , степень которых не превосходит 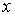 . Такую функцию . Такую функцию 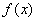 называют функцией Поша графа называют функцией Поша графа  . .
Для примера построим функцию Поша
следующего графа:
Функция будет
описано таблично:
|
x
|
0
|
1
|
2
|
3
|
4
|
5
|
...
|
|
f(x)
|
0
|
1
|
3
|
4
|
4
|
4
|
...
|
Теперь сформулируем условие Поша.
Графом
Поша называется граф  , удовлетворяющий следующим условиям (число вершин этого
графа обозначим через , удовлетворяющий следующим условиям (число вершин этого
графа обозначим через 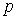 , его функцию Поша обозначим через , его функцию Поша обозначим через 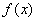 , символ , символ 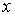 будет обозначать целое
число): будет обозначать целое
число):
1)
для 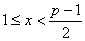 выполняется
неравенство выполняется
неравенство 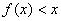 ; ;
2)
если 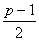 - целое число, то при - целое число, то при 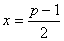 имеет место неравенство: имеет место неравенство:
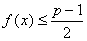 . .
Можно доказать, что каждый граф Поша обязательно гамильтонов.
Легко заметить, что простой цикл на большом числе вершин графом Поша не
является, но, конечно, является гамильтоновым графом.
Кроме того, нетрудно заметить, что всякий граф Дирака является графом Поша.
То же верно и в отношении графов Оре:
каждый граф Оре является графом Поша. Обратное в обоих последних случаях
неверно. Вот пример: фиксируем
какой-нибудь полный граф на достаточно большом числе вершин; добавим к нему еще
одну вершину и соединим ее с любыми двумя вершинами в исходном графе; очевидно,
вновь полученный граф - гамильтонов; фиксируем
в нем
какой-нибудь гамильтонов цикл и удалим из графа какое-нибудь ребро, не
включенное в этот цикл; полученный в результате граф будет, как нетрудно
проверить, графом Поша; однако, он не будет графом Оре - будут сразу две пары
несмежных вершин, сумма степеней которых меньше числа вершин в графе.
Лекция 6
Формулировка
теоремы Менгера (вершинный и реберный варианты), теорема Холла о системах
различных представителей и теорема Кёнига о независимых клетках в матрице.
Пусть  - некоторый граф и - некоторый граф и  , причем , причем 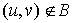 (т.е. вершины (т.е. вершины  не являются смежными).
Набор вершин не являются смежными).
Набор вершин 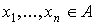 называется ( называется ( )-разделяющим, если
после удаления из графа всех вершин набора вершины )-разделяющим, если
после удаления из графа всех вершин набора вершины  оказываются
несвязанными (т.е. ока- оказываются
несвязанными (т.е. ока-
зываются в
разных связных компонентах). Если исходный граф связен, то для каждой пары
несмежных вершин 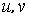 возникает следующая
характеристика: минимальное число ( возникает следующая
характеристика: минимальное число ( )-раз-деляющих вершин;
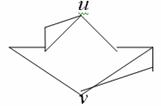
будем в длижайшем тексте обозначать это число символом k. Например, в приведенном ниже графе это число равно двум, хотя
( )-раз-деляющих вершин;
будем в длижайшем тексте обозначать это число символом k. Например, в приведенном ниже графе это число равно двум, хотя
( )-разделяющих наборов здесь не-сколько: )-разделяющих наборов здесь не-сколько:
Будем, далее, всякую цепь,
соединяющую вершины 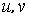 называть ( называть ( )-цепью; если у
двух ( )-цепью; если у
двух ( )-цепей имеется общая вершина, отличная от )-цепей имеется общая вершина, отличная от  , то будем называть такие две ( , то будем называть такие две ( )-цепи вершинно пересекающимися.
Очевидно, в каждом графе для данных двух вершин )-цепи вершинно пересекающимися.
Очевидно, в каждом графе для данных двух вершин  существует следующая
характеристика - максимальное число
вершинно-неперсекающихся (попарно) ( существует следующая
характеристика - максимальное число
вершинно-неперсекающихся (попарно) ( )-цепей. Будем в
этом тексте обозначать только что введенную характеристику через l.
Нетрудно понять, что всегда )-цепей. Будем в
этом тексте обозначать только что введенную характеристику через l.
Нетрудно понять, что всегда 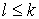 . Сформулируем теперь теорему
Менгера: всегда . Сформулируем теперь теорему
Менгера: всегда 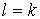 . Или
то же самое словами: минимальное число ( . Или
то же самое словами: минимальное число ( )-разделяющих вершин
равно максимальному числу вершинно непересекающихся (попарно) ( )-разделяющих вершин
равно максимальному числу вершинно непересекающихся (попарно) ( )-цепей. )-цепей.
Сформулированная
только что теорема называется вершинным вариантом
теоремы Менгера. Существует аналогичный реберный вариант этой теоремы.
Сформулируем его.
В прежних обозначениях набор ребер 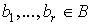 называется ( называется ( )-разделяющим, если
после удаления этих ребер из графа вершины )-разделяющим, если
после удаления этих ребер из графа вершины  окажутся несвязанными
(т.е. в разных связных компонентах). Ясно, что граф обладает следующей
характеристикой: минимальное число ребер,
составляющих ( окажутся несвязанными
(т.е. в разных связных компонентах). Ясно, что граф обладает следующей
характеристикой: минимальное число ребер,
составляющих ( )-разделяющий набор.
Обозначим эту характеристику через k. )-разделяющий набор.
Обозначим эту характеристику через k.
Назовем, далее, набор (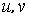 )-цепей реберно
непересекающимся (а цепи этого набора -
реберно непересекающимися), если любые две цепи набора не имеют общих
ребер. Очевидно, для каждого графа и фиксированных в нем вершин )-цепей реберно
непересекающимся (а цепи этого набора -
реберно непересекающимися), если любые две цепи набора не имеют общих
ребер. Очевидно, для каждого графа и фиксированных в нем вершин  существует такая
характеристика: максимальбное число
реберно непересекающихся ( существует такая
характеристика: максимальбное число
реберно непересекающихся ( )-цепей. )-цепей.
Обозначим эту
характеристику через l. Как и в предыдущем случае, очевидно,
что 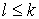 . Реберный вариант
теоремы Менгера: всегда . Реберный вариант
теоремы Менгера: всегда 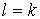 (или
словами: минимальное число ( (или
словами: минимальное число ( )-разделяющих ребер
равно максимальному числу реберно непересекающихся ( )-разделяющих ребер
равно максимальному числу реберно непересекающихся ( )-цепей. )-цепей.
Мы продемонстрируем на двух примерах
плодотворность теоремы Менгера (в обоих е вариантах - вершинном и реберном).
Пример 1. Теорема Холла о системах различных
представителей. Пусть 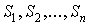 - некоторые множества
и имеются элементы - некоторые множества
и имеются элементы 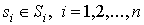 ;
элементы ;
элементы 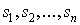 называются системой различных представителей, если
все они попарно различны. называются системой различных представителей, если
все они попарно различны.
Если рассмотреть множества 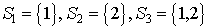 , то станет ясно, что система различных представителей
существует не всегда. Теорема Холла утверждает: система множеств , то станет ясно, что система различных представителей
существует не всегда. Теорема Холла утверждает: система множеств 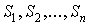 обладает системой различных представителей тогда и только тогда, когда
в объединении любых k множеств из числа данных обладает системой различных представителей тогда и только тогда, когда
в объединении любых k множеств из числа данных 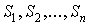 имеется k
различных элементов, имеется k
различных элементов, 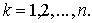
Для доказательства этого факта
строится следующий граф:
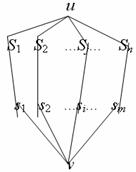
Здесь 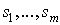 - элементы,
составляющие объединение - элементы,
составляющие объединение 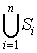 , а ребро , а ребро 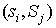 включается тогда и
только тогда, когда включается тогда и
только тогда, когда 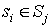 . Именно в этом графе факт того, что минимальное число . Именно в этом графе факт того, что минимальное число 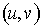 -разделяющих вершин равно максимальному числу вершинно
непересекающихся -разделяющих вершин равно максимальному числу вершинно
непересекающихся 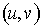 -це-пей, можно проинтерпретировать как то, что система
различных представителей существует тогда и только тогда, когда в объединении
любых k
множеств содержится не
менее k различных элементов. -це-пей, можно проинтерпретировать как то, что система
различных представителей существует тогда и только тогда, когда в объединении
любых k
множеств содержится не
менее k различных элементов.
Пример
2. Теорема Кёнига о покрывающих линиях. Пусть имеется некоторая
матрица 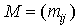 , в которой все элементы равны либо нулю, либо единице. Будем
словом линия обозначать либо строку, либо
столбец в данной матрице. Две единицы в матрице будем называть независимыми, если они не находятся на
одной линии. Произвольный набор единиц будем называть набором независимых единиц, если любые две единицы в наборе
независимы. Наконец, набор линий в данной матрице будем называть покрывающим, если каждая единица матрицы
принадлежит хоть одной линии набора. , в которой все элементы равны либо нулю, либо единице. Будем
словом линия обозначать либо строку, либо
столбец в данной матрице. Две единицы в матрице будем называть независимыми, если они не находятся на
одной линии. Произвольный набор единиц будем называть набором независимых единиц, если любые две единицы в наборе
независимы. Наконец, набор линий в данной матрице будем называть покрывающим, если каждая единица матрицы
принадлежит хоть одной линии набора.
Теорема
Кёнига утверждает: максимальное число
независимых единиц матрицы равно минимальному числу линий, составляющих покрывающий
набор.
Для доказательства и этой теоремы
строится такой же граф, как и для теоремы Холла (он изображен на последнем
рисунке) с той лишь разницей, что 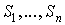 становятся именами
строк данной матрицы, становятся именами
строк данной матрицы, 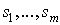 - становятся именами
столбцов и ребро - становятся именами
столбцов и ребро 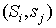 включается включается
тогда и только
тогда, когда на пересечении i-ой строки и j-ого столбца
стоит в матрице единица. Факт, сформулированный в теореме Кёнига, именно в этой
матрице превращается в вершинный вариант теоремы Менгера в отношении вершин 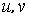 . .
|