|
Лабораторная работа №3
Оптимизация затрат ресурсов
в производственной деятельности
Цель работы: Определение оптимальных затрат ресурсов в различных
производственных условиях.
1. Краткие теоретические
сведения
В лабораторной работе №2
было введено понятие изокванты. Неоклассическая теория фирмы построена на
предположении, что цель фирмы заключается в максимизации прибыли путем выбора
затрат при заданной функции  и заданных ценах
выпуска и заданных ценах
выпуска  и ценах затрат и ценах затрат  и и  . В качестве функции издержек выбирают выражение . В качестве функции издержек выбирают выражение  , где , где  –
фиксированные издержки, –
фиксированные издержки,  –
переменная часть затрат, которая регулируется. –
переменная часть затрат, которая регулируется.
Геометрическое место точек,
для которых издержки постоянны,  , называется изокостами. Изокосты представляют собой
параллельные прямые с наклоном , называется изокостами. Изокосты представляют собой
параллельные прямые с наклоном
 (1)
(1)
Траектория точек касания
изоквант и изокост указывает такое сочетание ресурсов, при котором затраты,
необходимые для каждого из выпусков, минимальны. Геометрическое место
пересечения изокост и изоквант определяет долгосрочный путь решения.
Так
как изокванты имеют наклон
 (2)
(2)
то уравнение долгосрочного пути расширения получается путем приравнивания
правых частей соотношений (1) и (2)
 (3) (3)
Используя полученный из
уравнения (3) путь расширения  , можно получить кривую издержек , можно получить кривую издержек  , характеризующую минимальные издержки при различных условиях
выпуска. Для этого соотношение , характеризующую минимальные издержки при различных условиях
выпуска. Для этого соотношение  подставляется в
уравнение подставляется в
уравнение  . C использованием полученного равенства может быть
определена функциональная зависимость . C использованием полученного равенства может быть
определена функциональная зависимость  и и 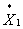 от выпуска. от выпуска.
Подставляя эти зависимости в
функцию издержек, можно получить уравнение издержек (функции производственных
затрат)  . Средние и предельные издержки определяются соответственно
как . Средние и предельные издержки определяются соответственно
как
 , ,  . .
Таким образом, исходя из
планируемого выпуска  , можно определить издержки , можно определить издержки  и оптимальные затраты
ресурсов и оптимальные затраты
ресурсов
 и и  . .
Если величина выпуска
определяется исходя из максимизации прибыли
 , (4) , (4)
то
 , (5) , (5)
т.е. предельные затраты равны цене
выпуска. Тогда величина выпуска, максимизирующая
прибыль, является решением уравнения
(5). Затем определяется оптимальное значение затрат ресурсов  и и 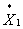 , как функций цены выпуска , как функций цены выпуска  и цен
затрат и цен
затрат  и и  . Подставляя . Подставляя  и и  в производственную функцию в производственную функцию  получим функцию
предложения выпуска получим функцию
предложения выпуска
 . .
2. Порядок выполнения работы
1. Составить программу, которая
изображает на экране дисплея: Четыре изокванты,
касательными к которым служат четыре изокосты и определить
такое сочетание ресурсов, при
котором затраты, необходимые для каждого выпуска,
минимальны. Построить траекторию точек касания изоквант и
изокост (долгосрочный путь расширения).
2. Составить программу, которая
изображает кривую издержек, средние и предельные издержки. Дать анализ
полученных кривых.
3. Определить объем выпуска,
максимизирующего прибыль.
3. Контрольные вопросы
1. Как изменяется положение
изокосты, если 1-го ресурса увеличивается вдвое?
2. Как предприятие выбирает
вектор затрат  и и  , решая долгосрочную задачу расширения производства? , решая долгосрочную задачу расширения производства?
3. Что называется издержками
производства?
4. Как определить минимальные
издержки и оптимальное распределение ресурсов при планируемом выпуске?
5. Указать на графике кривых
предельных издержек, соответствующую выпуску, максимизирующему прибыль при
заданных ценах.
4. Литература
1. М. Интрилигатор. Математические
методы оптимизации и экономическая теория. М., Прогресс, 1975.-606 с.
2. У. Баумоль. Экономическая
теория и исследование операций. М., Прогресс, 1965.-512 с.
3.
Математическая экономика на персональном компьютере. Пер. с японского
(Под редакцией М. Кубонива). М., Финансы и статистика, 1991,-303 с.
|