|
№2. Основные модели краткосрочного
страхования жизни(n=19).
Задача 1.
Обозначим за 1 величину, равную 250 000 р., т.е.
страховой выплате.
Распределение случайной величины x,
равной страховой выплате по одному контракту, выглядит следующим образом.
По формуле
Бернулли найдём распределение суммарного иска за год.
|
s
|
0
|
1
|
2
|
3
|
4
|
5
|
|
p
|
0,18042
|
0,36847
|
0,30100
|
0,12294
|
0,02511
|
0,00205
|
Нетто-премия
равна математическому ожиданию страховой выплаты, т.е.
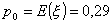  или в рублях получаем или в рублях получаем 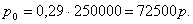
Для нахождения
величины страховой премии, чтобы вероятность разорения не превосходила 10%,
найдём вероятность 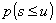 при разных значениях
капитала страховой компании (u). при разных значениях
капитала страховой компании (u).
|
u
|
[0;1)
|
[1;2)
|
[2;3)
|
[3;4)
|
|
p(s£u)
|
0,18042
|
0,54889
|
0,84990
|
0,97284
|
Дальнейшее нахождение вероятности 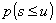 при разных значениях
капитала страховой компании не имеет смысла, т.к. при u=3 p(s£u)=0,97284. Отсюда величина страховой
премии, чтобы вероятность разорения не превосходила 10%, равна при разных значениях
капитала страховой компании не имеет смысла, т.к. при u=3 p(s£u)=0,97284. Отсюда величина страховой
премии, чтобы вероятность разорения не превосходила 10%, равна 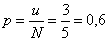 или в рублёвом
выражении p=0,6×250000=150000
р. или в рублёвом
выражении p=0,6×250000=150000
р.
Задача 2.
Обозначим за 1
величину, равную 250 000 р.
Распределение случайной величины x,
равной страховой выплате по одному контракту, выглядит следующим образом.
Нетто-премия
равна математическому ожиданию страховой выплаты, т.е.
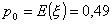  или в рублях получаем или в рублях получаем 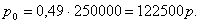
a)
Найдём распределение суммарного иска, используя
свертки.
Пусть случайная
величина m1=x1+x2,
а m2=x3+x4.
Суммарный иск S=m1+m2.
|
x1+x2
|
0
|
1
|
2
|
3
|
4
|
|
p
|
0,3721
|
0,3538
|
0,2061
|
0,058
|
0,01
|
Построим
распределение суммарного иска:
|
S
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
p
|
0,13846
|
0,26330
|
0,27855
|
0,18900
|
0,09096
|
0,03098
|
0,00749
|
0,00116
|
0,00010
|
Для нахождения
величины страховой премии, чтобы вероятность разорения не превосходила 10%,
найдём вероятность 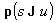 при разных значениях
капитала страховой компании (u). при разных значениях
капитала страховой компании (u).
|
u
|
[0;1)
|
[1;2)
|
[2;3)
|
[3;4)
|
[4;5)
|
|
p(s£u)
|
0,13846
|
0,40176
|
0,68031
|
0,86931
|
0,96027
|
Дальнейшее нахождение вероятности 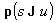 при разных значениях
капитала страховой компании не имеет смысла, т.к. при u=4 p(s£u)=0,96027. Отсюда величина страховой
премии, чтобы вероятность разорения не превосходила 10%, равна при разных значениях
капитала страховой компании не имеет смысла, т.к. при u=4 p(s£u)=0,96027. Отсюда величина страховой
премии, чтобы вероятность разорения не превосходила 10%, равна 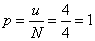 или в рублёвом
выражении p=250000р. или в рублёвом
выражении p=250000р.
b)
Найдём распределение суммарного иска с помощью
производящих функций.
Построим производящую функцию случайной величины xi:
Производящая
функция для суммарного иска выглядит следующим образом:
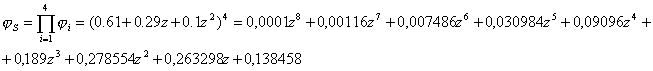
Как и следовало ожидать, распределения суммарного
риска, полученные с помощью свёрток и производящих функций, полностью совпали.
Поэтому все результаты аналогичны значениям пункта а).
Задача 3.
Обозначим за 1
величину, равную 250 000 р.
Случайные величины
x39
и x49
- страховые выплаты по одному контракту для застрахованных в возрасте 39 и 49
лет соответственно.
Вероятность смерти застрахованных лиц в течении
года найдём из таблицы продолжительности жизни.
Распределения
случайных величин x39
и x49
выглядят следующим образом:
|
x39
|
0
|
1
|
|
p
|
0,996858
|
0,003142
|
|
x49
|
0
|
1
|
|
p
|
0,994448
|
0,005552
|
Нетто-премии
соответственно равны:
P39|0=0,003142 или в рублях
получаем P39|0=785,5
р.,
P49|0=0,005552 или в рублях
получаем P49|0=1388
р.
a)
Вычислим страховую премию, гарантирующую вероятность
разорения не более 5%, используя приближение Пуассона.
l=2000×0,003142+500×0,005552=9,06»9;
a=95%.
Из таблицы
находим xa: xa=.
Вычислим
страховые премии, гарантирующие вероятность разорения не более 5%, для
застрахованных в возрастах 39 и 49 лет.
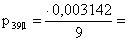 или в рублях получаем или в рублях получаем 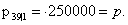
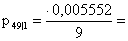 или в рублях получаем или в рублях получаем 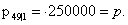
b)
Вычислим страховую премию, гарантирующую вероятность
разорения не более 5%, используя приближение Гаусса.
E[s]=l=9,06»9;
Var s= 2000×0,996858×0,003142+500×0,994448×0,005552=9,0248»9
При a=95% xa=
Сейчас найдём
капитал, обеспечивающий с 95% вероятность неразорения: 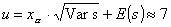
Вычислим
страховые премии, гарантирующие вероятность разорения не более 5%, для
застрахованных в возрастах 39 и 49 лет
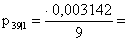 или в рублях получаем или в рублях получаем 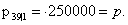
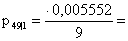 или в рублях получаем или в рублях получаем 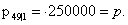
Задача 4.
Обозначим за 1
величину, равную 250 000 р.
Распределение случайной величины x,
равной страховой выплате по одному контракту, выглядит следующим образом.
|
x
|
0
|
1
|
3
|
|
p
|
0,9966
|
0,0029
|
0,0005
|
Нетто-премия
равна математическому ожиданию страховой выплаты, т.е.
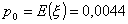 или в рублях получаем или в рублях получаем 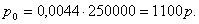
Предположим,
что суммарный иск имеет распределение Гаусса. Тогда найдём xa из
уравнения F(xa)=0,985
(xa»2,17).
Таким образом,
капитал, обеспечивающий с 98,5% вероятность неразорения, равен: 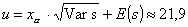 , где E(s)=5000×(0,0029+0,0005×3)=22, , где E(s)=5000×(0,0029+0,0005×3)=22,
Var s=5000×(E(x2)-
[E(x)]2)= 36,9032.
Вычислим
страховую премию, гарантирующую вероятность разорения не более 5,75%:
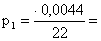 или в рублях получаем или в рублях получаем 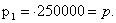
Относительная страховая надбавка равна: 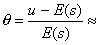
|