§ 2. Цепные дроби
Пункт 9. Свойства подходящих дробей.
Это сложный пункт, в нем будет мало слов крупным шрифтом. Взгляните еще раз на название пункта, и "поехали" (цитата из литературного наследия Ю. Гагарина, точнее, это литературное наследие здесь процитировано полностью).
Свойство 1 . P s Q s -1 - Q s P s -1 = (- 1) s , s > 0.
Доказательство. Обозначим h s = P s Q s -1 - Q s P s -1 .
h 1 = P 1 Q 0 - Q 1 P 0 = q 1 · 0 - 1 · 1 = -1,
h
s
=
P
s
Q
s
-1
-
Q
s
P
s
-1
=
= (
q
s
P
s
-1
+
P
s
-2
)
Q
s
-1
- (
q
s
Q
s
-1
+
Q
s
-2
)
P
s
-1
=
=
P
s
-2
Q
s
-1
-
Q
s
-2
P
s
-1
= -
h
s
-1
.
Значит, h s = (-1) s .
Ё
Свойство 2.
| d s - d s -1 = |
(-1)
s
Q s Q s -1 |
, s > 1. |
Доказательство.
| d s - d s -1 = |
P
s
Q s |
= |
P
s
-1
Q s -1 |
= |
h
s
Q s Q s -1 |
= |
(-1)
s
Q s Q s -1 |
. Ё |
Свойство 3. Для любого s > 0, дробь P s / Q s - несократима.
Доказательство. Ну пусть наибольший общий делитель ( P s , Q s ) равен d и d > 1. Тогда d делит разность P s Q s -1 - Q s P s -1 , равную (-1) s , что невозможно.
Ё
Свойство 4.
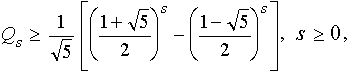
и равенство достигается только при q 1 = q 2 =...= q s = 1.
Доказательство. Нам уже известно, что
Q 0 = 0, Q 1 = 1, q i О N , Q s = q s Q s -1 + Q s -2 і Q s -1 + Q s -2 .
Наиболее медленный рост знаменателей будет наблюдаться при Q s = Q s -1 + Q s -2 , т.е. при q 1 = q 2 = ... = q s = 1. Это рекуррентное соотношение вместе с начальными условиями Q 0 = 0, Q 1 = 1 задает последовательность Фибоначчи. Характеристическое уравнение для рекуррентного соотношения Фибоначчи:
x 2 = x + 1;
| его корни: x 1,2 = |
1±
Ц
5
2 |
; |
общее решение:
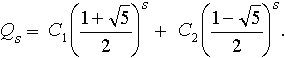
Подстановка начальных условий в общее решение дает
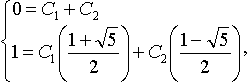
откуда C 1 = - C 2 = 1/ Ц 5.
Впрочем, формула s -ого члена последовательности Фибоначчи достаточно общеизвестна, ее вывод можно посмотреть, например, в брошюрах А. И. Маркушевича "Возвратные последовательности" или Н. Н. Воробьева "Числа Фибоначчи" из серии "Популярные лекции по математике", регулярно выходившей для школьников в издательстве "Наука".
Итак, знаменатели подходящих дробей растут не медленнее последовательности Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,...
Ё
Отступление про Фибоначчи.
Фибоначчи - "Сын Боначчо" или Леонардо Пизанский (1180 - 1240), - известный средневековый математик-кроликовод, философ, купец и т.д. Путешествовал и торговал в странах востока, но, в отличие от тупых современных челноков, озабоченных только марксовской разностью Д ў - Д, где Д - деньги, Д ў - деньги штрих, изучал науку востока. По возвращению в Европу он записал собранные сведения, добавил много собственных исследований и издал книги "Практика геометрии" и "Книга абака". Последовательность Фибоначчи возникает у самого Леонардо при решении следующей задачи: Сколько пар кроликов может произойти от одной пары в течении года, если а) каждая пара каждый месяц порождает новую пару, которая со второго месяца становится производителем, и б) кролики не дохнут. Поразительным образом, демонстрируя единство мироздания, последовательность Фибоначчи появляется не только при изучении цепных дробей, но и во многих других разделах математики, физики, биологии, искусствоведения. Кроме порождения на свет этой замечательной последовательности и другого прочего, "Книга абака" была одним из решающих источников проникновения в Западную Европу десятичной системы счисления и арабской записи цифр. Честь и хвала безумцам, которые, порой в ущерб своему благосостоянию, сохраняют и развивают культуру целых поколений, безумцам, чья система ценностей не замкнута на шмотках, деньгах и развлечениях!
Свойство 5. Для любой бесконечной цепной дроби, последовательность d 1 , d 2 , d 3 ,... сходится.
Доказательство. Рассмотрим подпоследовательности:
|
P
0
Q 0 |
, |
P
2
Q 2 |
, ... , |
P
2
n
Q 2 n |
, ... - дроби с четными номерами и |
|
P
1
Q 1 |
, |
P
3
Q 3 |
, ... , |
P
2
n
+1
Q 2 n +1 |
, ... - дроби с нечетными номерами. |
Имеем:
|
P
2
n
+2
Q 2 n +2 |
- |
P
2
n
Q 2 n |
= d 2 n +2 - d 2 n +1 + d 2 n +1 - d 2 n = |
| = |
1
Q 2 n +2 Q 2 n +1 |
+ |
-1
Q 2 n +1 Q 2 n |
< 0, |
т.к. Q 2 n +2 Q 2 n +1 > Q 2 n +1 Q 2 n . Значит, подпоследовательность дробей с четными номерами монотонно убывает. Аналогично, вторая подпоследовательность монотонно возрастает. Всякий член "четной" последовательности больше всякого члена "нечетной". Действительно, рассмотрим d 2 n и d 2 m +1 . Возьмем четное k такое, что k +1 > 2 n и k +1 > 2 m + 1. Тогда
| d k - d k -1 = + |
1
Q k Q k -1 |
> 0, т.е. d k > d k -1 . |
Но ведь d k < d 2 n , в силу убывания последовательности "четных", а d k -1 > d 2 m +1 , в силу возрастания последовательности "нечетных". Значит, d 2 n > d k > d k -1 > d 2 m +1 , что и нужно. Получается, что обе последовательности монотонны и ограничены, следовательно, имеют пределы. Кроме того,
| | d s - d s -1 | = |
1
Q s Q s -1 |
< |
1
F s F s -1 |
—— ® s ®Ґ |
0, |
где F s - s -ый член последовательности Фибоначчи, следовательно пределы обеих подпоследовательностей совпадают.
Итак, всякая бесконечная цепная дробь имеет некоторое значение.
Ё
Свойство 6. Пусть a О R раскладывается в цепную дробь, например, с помощью процесса взятия целых частей и "переворачивания" дробных (этот процесс предложен в пункте 7 после формулировки основной теоремы о цепных дробях), т.е.
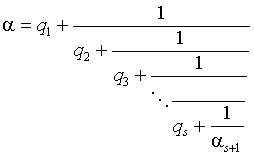
- результат очередного этапа процесса разложения. Тогда a лежит между d s -1 и d s , причем ближе к d s , чем к d s -1 .
Доказательство. На ( s +1)-ом шаге разложения мы заменяем q s на q s + 1/ a s +1 , поэтому имеем точное равенство:
| a = |
a
s
+1
P
s
+
P
s
-1
a s +1 Q s + Q s -1 |
, значит |
a a s +1 Q s + a Q s -1 - a s +1 P s - P s -1 = 0.
Преобразуем:
| a s +1 Q s |
ж
з и |
a - |
P
s
Q s |
ц
ч ш |
+ Q s -1 |
ж
з и |
a - |
P
s
-1
Q s -1 |
ц
ч ш |
= 0. |
Это равенство означает, что разности в скобках разных знаков. Кроме того, Q s > Q s -1 , a s +1 > 1, значит
|
з
з з |
a - |
P
s
Q s |
з
з з |
< |
з
з з |
a - |
P
s
-1
Q s -1 |
з
з з |
. Ё |
Свойство 7. Для любого a О R , разложение в цепную дробь единственно.
Доказательство. Пусть есть два разложения одного и того же числа:
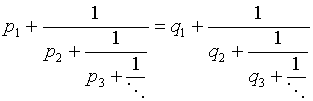
Если два числа совпадают, то у них совпадают целые части, т.е. р 1 = q 1 , и совпадают обратные величины к дробным частям:
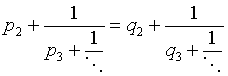
Далее точно так же, по индукции.
Ё

Наблюдательный читатель уже наверняка заметил, что основная теорема о цепных дробях (сформулированная в пункте 7), о необходимости доказательства которой так долго говорили большевики, к этому моменту оказалась доказанной. Более того, из вышеизложенного следует, что всякая цепная дробь (конечная или бесконечная) сходится именно к тому числу, которое было в нее разложено. И слава Богу! Аллилуйя!
Задачки

|
1 . Найдите формулу n -ого члена последовательности, задаваемой рекуррентно: a n = a n -1 + 2 a n -2 ; a 1 = 0, a 2 = 6. 2 . Продвинутый десятиклассник Петя решает на школьной олимпиаде такую задачу: Доказать, что при любом n = 0, 1, 2,..., число
является целым. Поскольку Петя знает только бином Ньютона, у него получаются очень громоздкие вычисления, в которых он тонет. Помогите Пете, не используя бином Ньютона. 3 . Вычислите a с точностью до десятого знака после запятой, если: а) a = Ц 2; б) a = Ц 5. Разрешается использовать только ваше умение оценивать разность между соседними подходящими дробями и калькулятор, умеющий выполнять сложение, умножение, вычитание и деление. 4 . Вычислив последнюю и предпоследнюю подходящие дроби числа 215/157, решите диофантовы уравнения: а) 215 x - 157 y = 1; б) 215 x - 157 y = 4. |
| NS | НОВОСТИ КУЛЬТУРЫ |
|
В Третьяковской галерее отреставрирована известная картина Репина "Бурлаки на Волге". Теперь она называется "Бурлаки на Мерседесе". В серии "Раскрась сам" издательство "Плоды просвещения" выпустило для самых маленьких книжку-раскраску "Импрессионисты рубежа 19-20 веков". Учитесь правильно говорить. Нужно говорить не "ложить", а "класть". Например: - Мадам, кладите себе сахар в чай, пожалуйста. Ответ: - Спасибо, я уже наклала. Популярный актер Невинный заказал скульптору Неизвестному слепить Непонятное. Выдающийся кинорежиссер А. Хичкок, основоположник жанра фильмов-ужасов, просмотрев на последнем кинофестивале фильм режиссера Пупочкина, воскликнул: "Какой ужас!" |
|