§5. Трансцендентные числа.
Пункт 28. Трансцендентность значений функции ez.
Последний пункт нашей книжки имеет номер 28 - второе совершенное число и посвящен обсуждению одного замечательного свойства показательной функции.
Теорема (Линдеман). Если x - алгебраическое число и x№0 , то число ex - трансцендентно.
Поразительно, правда? Точки координатной плоскости с рациональными координатами всюду плотно заполняют эту плоскость, точки с обеими алгебраическими координатами (алгебраические точки) - тем более. Однако сплошная и ровная кривая - график функции y=ex , не дергаясь из стороны в сторону, проходит спокойно и величаво между всеми алгебраическими точками, случайно раздавив только одну - (0, 1).
Из теоремы Линдемана также вытекает, например, что число ln 2 – трансцендентно, ведь 2=eln 2, а число 2 - алгебраическое. Оказывается, мы еще в средней школе видели массу трансцендентных чисел - ln 2, ln 3, ln ( 5Ц27) и т.п. – и совершенно не подозревали об этом. От нас скрывали правду! Это вопиющее нарушение прав человека и, в частности, ребенка. ООН! SOS! OON! СОС! Но прекратим орать на разных языках и перейдем к делу.
Доказательство теоремы Линдемана можно провести с помощью тождества Эрмита, аналогично тому, как была доказана трансцендентность p, с некоторыми усложнениями в преобразованиях. Именно так ее и доказывал сам Линдеман. Однако я пойду другим путем, ибо хочу познакомить читателей с основными идеями советского математика А. О. Гельфонда, приведшими в середине ХХ века к решению Седьмой проблемы Гильберта - проблеме о природе чисел вида ab, где a,b - алгебраические и b - иррационально. Чтобы не дразнить ваше любопытство, скажу сразу, что числа вида ab, где a,b - алгебраические и b - иррационально (например, 2Ц2), являются трансцендентными, но мы этого доказывать не будем, так как от этого наша маленькая книжка по теории чисел может сразу превратиться в большую.
Доказательство трансцендентности значений показательной функции, предложенное Гельфондом, основывается на применении интерполяционных методов. В этом доказательстве, с помощью разложения функции exЧz в интерполяционный ряд Ньютона, строится последовательность многочленов Pn(x,y) c целыми коэффициентами такая, что |Pn(x,ex)| достаточно быстро убывает с ростом n . Однако несложно получить оценку снизу значения произвольного многочлена с целыми коэффициентами от двух произвольных алгебраических чисел, поэтому предположение об алгебраичности чисел x и ex породит противоречие между верхней и нижней оценками. Далее будут представлены три основных этапа доказательства Гельфонда: построение ряда Ньютона функции exЧz, построение многочленов Pn(x,y) и их оценка сверху, оценка |Pn(x,ex)| снизу и сопоставление полученных оценок. Приступим.
Этап 1. Интерполяционный ряд Ньютона функции exЧz.
Пусть функция f(z) аналитическая в области D, точки z1,z2,...,znОD - фиксированы и, быть может, среди них есть совпадающие. Положим
F0(t)=1, Fk=(t-z1)(t-z2)...(t-zk); k=1,2,...,n.
Пусть zОD. При каждом k=1,2,...,n выполнено:
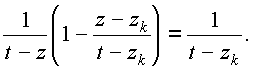
Умножим это тождество на Fk-1(z)/Fk-1(t). Получим:
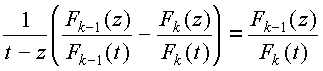 .
.
Сложим эти тождества:
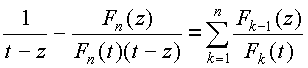
или
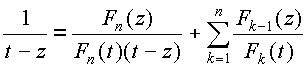
|
(Є) |
Пусть С - простой замкнутый контур в D, точки z1,z2,...,znОD лежат внутри этого контура. Умножим тождество (Є) на (1/ 2pi)f(t) и проинтегрируем, пользуясь формулой Коши:
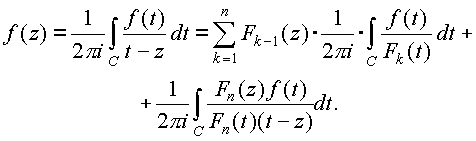
Обозначим:
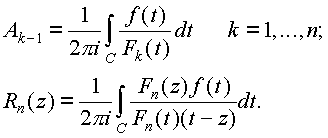
В этих обозначениях:
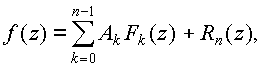
zОD
– интерполяционная формула Ньютона для функции f(z) с узлами интерполяции
z1,z2,...,zn. Если же z1,z2,...,zn,...
-
бесконечная последовательность узлов, а
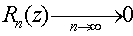 для всех zОD,
то
для всех zОD,
то
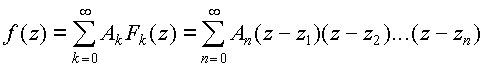
– интерполяционный ряд Ньютона для функции f(z) с узлами интерполяции z1,z2,...,zn,.... Нетрудно подсечь, что при z1=z2=...=zn=... из ряда Ньютона получается ряд Тейлора.
Пусть mОN. Хитрый Гельфонд взял за узлы интерполяции бесконечную периодическую последовательность периода m:
1, 2, 3, ..., m-1, m, 1, 2, ..., m-1, m, 1, 2, ...
т.е.
zn=n для n=1,2,...,m,
zn+lm = zn.
Разложим функцию f(z)=exЧz, где xОC, x№0, в ряд Ньютона с такими узлами интерполяции. Запишем формулу Ньютона:
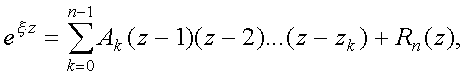
где:
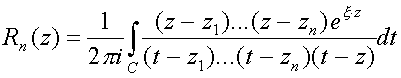
- остаточный член. Пусть R – любое число, такое, что R > m. Оценим остаточный член при n > 2R в круге |z|ЈR. Пусть С - окружность |t|=n. Имеем:
1ЈzkЈm,
следовательно,
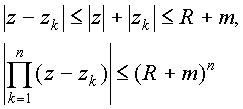
|
(1) |
для всех z из круга |z|ЈR. Далее, т.к. n>2R>2m, на окружности |t|=n имеем:
|t-zk|і|t|-|zk|іn-m> n/2
|t-z|і|t|-|z|іn-R> n/2
значит,
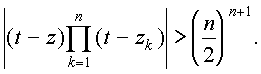
|
(2) |
Пользуясь неравенствами (1), (2), и неравенством |exЧt|Јe|x|Чn, оценим интеграл:
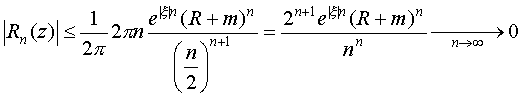
Число R может быть выбрано сколь угодно большим, поэтому при любом комплексном z, функция f(z)=exЧzпредставляется в виде суммы ряда Ньютона с целочисленной периодической последовательностью узлов интерполяции z1,z2,...,zn,...
Итак,
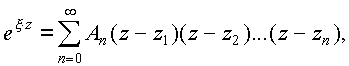
где
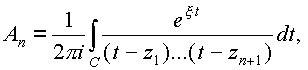
n=0,1,2,...
Выбирая за контур С окружность |t|=n, где n>2m, аналогично оценке остаточного члена в формуле Ньютона, получаем оценку сверху для коэффициентов ряда:
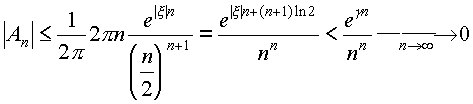 ,
,
где число g>0 и зависит только от x. Этап 1 завершен.
Этап 2. Построение многочленов Pn(x,y) и их оценка сверху.
Поскольку последовательность узлов интерполяции периодическая, то в произведении
Fn+1(t)=(t-1)(t-2)...(t-zn+1)
есть повторяющиеся сомножители. Обозначим число сомножителей вида (t-k) через nk+1. Тогда это произведение можно переписать так (подразумевается, что n>m):
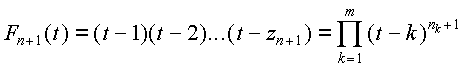 .
.
Ясно, что n1+n2+...+nm+m=n+1, и nk зависят от n . Кроме того, так уж устроена последовательность узлов интерполяции, что n1-1Ј nmЈ nm-1Ј ...Ј n1Ј n/m . Значит, коэффициенты ряда Ньютона можно записать так:
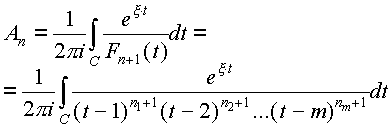 .
.
Окружим каждый узел интерполяции k (1Ј kЈm) окружностью Гk с центром в точке k и радиуса, например, 1/3. Эти окружности не пересекаются и лежат внутри контура С. Если зафиксировать на них положительное направление обхода, то, по теореме Коши,
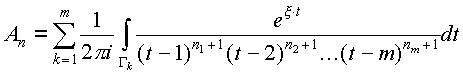 .
.
Обозначим h=ex. Разложим для каждого k (1ЈkЈm) функцию exЧ t в ряд Тейлора по степеням (t-k):
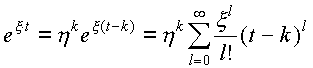 .
.
Тогда
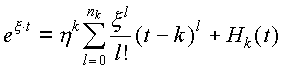 ,
,
где Hk(t) – остаточный член, являющийся целой функцией, имеющей в точке t=k нуль порядка nk+1. Это значит, что
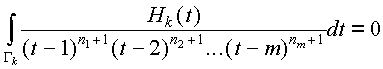 .
.
Тогда
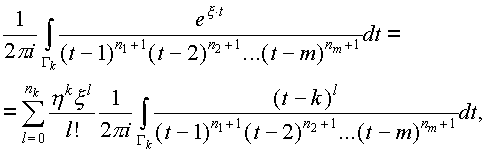
т.е. суммировать можно только до nk. Как мы лихо обрезали ряд Тейлора, несмотря на то, что Тейлор не ортодокс! Обозначим при каждом k (1ЈkЈm):
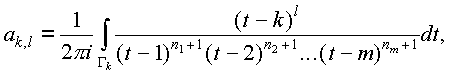 l=0,1,...,nk. |
(§) |
В этих новых обозначениях коэффициент ряда Ньютона выглядит так:
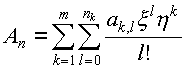 .
.
Пусть М - наименьшее общее кратное чисел 1,2,...,m. Сейчас я докажу, что все числа ak,l в коэффициенте An рациональные, а числа Mnak,l будут целыми. Число ak,l равно вычету в точке t=k подынтегральной функции из интеграла (§), т.е. равно коэффициенту при (t-k)-1 в разложении этой функции в ряд Лорана по степеням (t-k). Стиснем зубы и найдем это разложение.
Пусть sОN, 1ЈsЈm, s№k. Имеем:
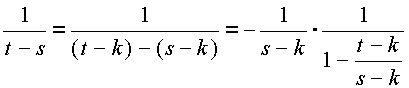 .
.
Если положить t-k=Mu и разложить функцию 1/(t-s) в ряд по степеням u, то получится:
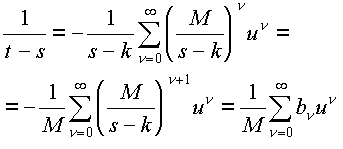 ,
,
где bn=-(M/ s-k)n+1. Этот ряд абсолютно сходится в круге |u| < |s-k|/M.
Очевидно, что числа bn=-(M/ s-k)n+1 целые, т.к. М– наименьшее общее кратное чисел 1,2,...,m, а число |s-k| – целое и 1Ј|s-k|Јm-1.
Теперь, для того, чтобы получилось нечто похожее на подынтегральное выражение из строчки (§), надо перемножать ряды
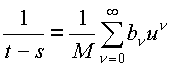
в подходящих степенях и при разных s. Произведение
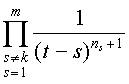
есть кусок подынтегрального выражения в (§) , оно отличается от самого подынтегрального выражения отсутствием множителя (t-k)l / (t-k)nk+1 = (t-k)l-nk-1. Стало быть, это произведение содержит (n1+1)+...+(nk-1+1)+(nk+1+1)+...+(nm+1)=n-nk сомножителей вида 1 / t-s. Посчитаем, наконец, это произведение:
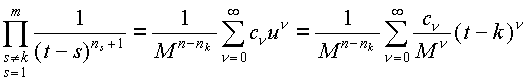 ,
,
где все cn, очевидно, целые числа, т.к. они есть суммы произведений целых bn (так уж ряды перемножаются, тут ничего не попишешь). Тогда подынтегральная функция в (§) равна
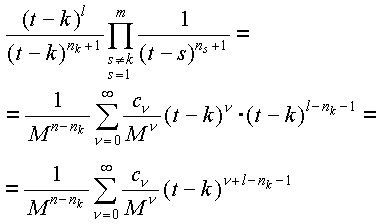
Это и есть искомое разложение в ряд Лорана. Нетрудно сообразить, что показатель n+l-nk-1 равен -1 при n=nk-l. Значит, искомый вычет есть
ak,l = cnk-l / Mn-l,
и является рациональным числом. Ну тогда, бесспорно, число Mnak,l - целое.
Далее все просто. Обратим снова свой взор на коэффициенты ряда Ньютона:
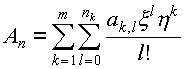 , ,
|
h=ex, |
Если обозначить через r=max nk=n1, 1ЈkЈm, то, очевидно, выражение
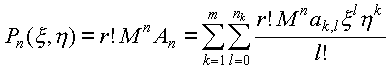
будет многочленом с целыми коэффициентами от двух переменных x и h, его степень по переменной x не превосходит r, а степень по переменной h не превосходит m. Это и есть те самые многочлены с целыми коэффициентами, которые мы запланировали построить на втором этапе нашего доказательства.
Оценим высоту Hn (максимум среди абсолютных величин коэффициентов) многочлена Pn. Помним, что
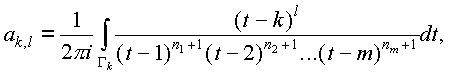
|
| l=0,1,...,nk, k=1,2,...,m |
Поскольку tОГk и радиус Гk мы взяли 1/3, то |t-k| < 1/2, а при s№k, |t-s| > 1/2. Значит,
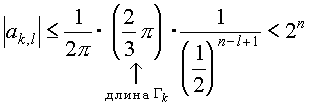
и высота Hn многочлена Pn удовлетворяет неравенству
Hn<r!(2M)r.
Оценим, наконец, |Pn(x,h)| сверху. В конце первого этапа мы получили оценку:
|An| < egn / nn = egn-nln n.
Поскольку Pn(x,h)=r!MnAn, а rЈn/m, то
|Pn(x,h)|<egn-nln n+nln M+rln r<e-(m-1 / m)nln n+Cn,
где С>0 - константа, не зависящая от n.
Этап 3. Оценка |Pn(x,h)| снизу.
Пусть a1,a2,...,am – алгебраические числа, Q – поле рациональных чисел, K=Q[a1,a2,...,am] - алгебраическое расширение поля Q, h - степень этого алгебраического расширения.
Напомню, что степенью алгебраического расширения называется степень примитивного минимального многочлена, корнями которого это расширение порождается. Это означает, что у каждого порождающего элемента поля K=Q[a1,a2,...,am] (примитивного элемента из K) имеется h штук сопряженных. В алгебраическом поле K=Q[a1,a2,...,am] степени h максимальное число линейно независимых над Q элементов равно h .
Сейчас мы докажем основной факт третьего этапа: Для любого многочлена с целыми коэффициентами P(z1,z2,...,zm) степени k и высоты H , существует постоянная c=c(a1,a2,...,am)>0 такая, что:
либо |P(a1,a2,...,am)| і ck/Hh-1,
либо P(a1,a2,...,am)=0.
Таким образом, алгебраические числа a1,a2,...,am произвольный многочлен с целыми коэффициентами либо обращают в ноль (в этом случае говорят, что числа a1,a2,...,am являются алгебраически зависимыми), либо значение этого многочлена находится достаточно далеко от нуля.
Пусть ai=ai(1),ai(2),...,ai(h)
– все сопряженные с ai в поле K=Q[a1,a2,...,am], 1ЈiЈm. Введем два обозначения. Через 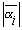 обозначим размер алгебраического числа ai,
обозначим размер алгебраического числа ai,
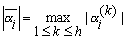 – максимальный из модулей чисел, сопряженных с ai. Через ||ai||K
обозначим норму алгебраического числа ai
в поле K, ||ai||K=ai(1),ai(2),...,ai(h) – произведение всех сопряженных
с ai. Проверьте сами, что ||ai||K действительно удовлетворяет
всем аксиомам нормы.
– максимальный из модулей чисел, сопряженных с ai. Через ||ai||K
обозначим норму алгебраического числа ai
в поле K, ||ai||K=ai(1),ai(2),...,ai(h) – произведение всех сопряженных
с ai. Проверьте сами, что ||ai||K действительно удовлетворяет
всем аксиомам нормы.
Еще одно замечание. Целым алгебраическим числом называется алгебраическое число, минимальный многочлен которого (у него старший коэффициент всегда единица) имеет целые коэффициенты. Так, например, Ц3 и 1+ Ц5 / 2- целые алгебраические числа, а - Ц3 / 2 не целое, т.к. их минимальные многочлены суть, соответственно, x2-3, x2-x-1 и x2 - 3/4. Если a - не целое алгебраическое число, то всегда можно подобрать некоторое натуральное число r такое, что ra будет корнем многочлена с целыми коэффициентами и старшим коэффициентом 1, т.е. будет целым алгебраическим числом. Множество целых алгебраических чисел поля K обозначим через ZK. Несложно проверить, что ZK - кольцо и всегда ZМZK.
Приступим к доказательству основного факта третьего этапа. Предположим, что P(a1,a2,...,am)№0. Подберем натуральное число r так, что raОZK, i=1,...,m. Так как многочлен Р степени k c целыми коэффициентами, то
b=rkP(a1,a2,...,am)ОZK, b№0.
Возможны два случая.
Случай 1. h=1 (т.е. K=Q ). Тогда
|b|=rk|P(a1,a2,...,am)|і1, |P(a1,a2,...,am)|і1 / rk.
Случай 2. h > 1. Обозначим
Aj=P(a1(j),a2(j),...,am(j)), j=1,...,h.
Числа A1,...,Ah будут сопряженными в поле K. По свойствам нормы
|||b||K|=|||rkA1||K|=rkh|A1A2...Ah|і1.
Отсюда вытекает, что
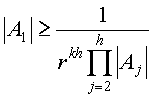 .
.
Если
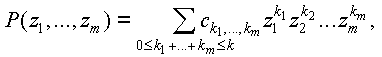
ck1,...,kmОZ,
то
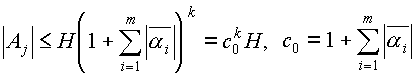 .
.
Ну, тогда из двух последних неравенств следует
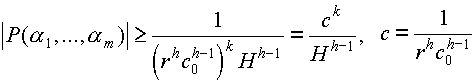 ,
,
а, собственно, это и требовалось доказать.
Наступил тот славный момент, когда у нас все готово для того, чтобы достойно завершить доказательство теоремы Линдемана. Давайте проделаем это. От противного. Ну пусть x№0 и h=ex - алгебраические числа, h - степень алгебраического расширения K=Q[x,h], h>1. Разложим exЧz в ряд Ньютона с периодической целочисленной последовательностью узлов интерполяции
1,2,...,m-1,m,1,2,...,m-1,m,1,2,... ,
где m=h+1. Построим наши пресловутые многочлены Pn(x,h). Мы только что доказали, что либо Pn(x,h)=0, либо
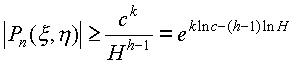
где (вспоминаем устройство многочленов Pn(x,h). Мы только что доказали, что либо Pn(x,h)=r!MnAn и оценку их высоты из второго этапа):
kЈr+m. HЈr ln r+n ln (2M), rЈn/m.
Отсюда моментально получается, что:
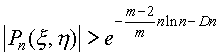
где D>0 - некоторая подходящая константа. Последнее неравенство и неравенство
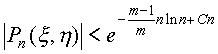 ,
,
полученное в конце второго этапа, при достаточно больших n противоречивы, значит, при всех достаточно больших n остается только возможность Pn(x,h)=r!MnAn. Это означает, что, начиная с некоторого номера, все An=0, т.е. ряд Ньютона функции exЧz содержит лишь конечное число членов и функция exЧz является многочленом. Но этого не может быть потому, что не может быть никогда. (Например, потому, что функция exЧz периодическая, а любой нетривиальный многочлен - нет). Этим и заканчивается доказательство теоремы Линдемана.
Ё
Закончился последний пункт нашей небольшой книжки по теории чисел, но я не буду говорить здесь никаких прощальных слов, ибо, как всегда во всех сказках, самое интересное только еще начинается. Идите вперед! Изучайте теорию чисел и она оправдает ваши надежды. Числа не подвержены инфляции, политическим и экономическим потрясениям, коррупции и обману. Математика не может приносить разочарований, она приносит только восхищение окружающим миром и человеческим разумом. Я желаю вам - Будьте счастливы!
