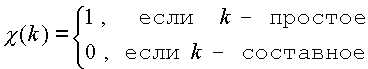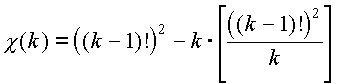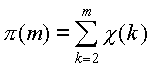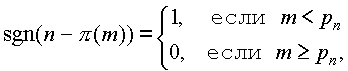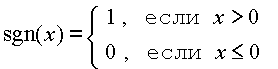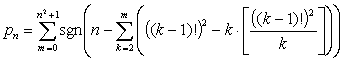§4. Теория сравнений

Пункт 20. Сравнения любой степени по простому модулю.

В этом пункте мы рассмотрим сравнения вида f(x) є 0(mod p) , где р - простое число, f(x)=ax n +a 1 x n-1 +…+a n - многочлен с целыми коэффициентами, и попытаемся научиться решать такие сравнения. Не отвлекаясь на посторонние природные явления, сразу приступим к работе.

Лемма 1. Произвольное сравнение f(x) є 0(mod p) , где р - простое число, равносильно некоторому сравнению степени не выше p-1 .

Доказательство. Разделим f(x) на многочлен x p -x (такой многочлен алгебраисты иногда называют "многочлен деления круга") с остатком: f(x)=(x p -x) Ч Q(x)+R(x), где, как известно, степень остатка R(x) не превосходит р-1 . Но ведь, по теореме Ферма, x p -x є 0(mod p) . Это означает, что f(x) є R(x)(mod p) , а исходное сравнение равносильно сравнению R(x) є 0(mod p).

Ё

Доказанная лемма приятна тем, что с ее помощью можно свести решение сравнения высокой степени к решению сравнения меньшей степени. Идем далее:

Лемма 2. Если сравнение ax n +a 1 x n-1 +…+a n є 0(mod p) степени n по простому модулю р имеет более n различных решений, то все коэффициенты a,a 1 ,…,a n кратны р .

Доказательство. Пусть сравнение ax n +a 1 x n-1 +…+a n є 0(mod p) , имеет n+1 решение и x 1 ,x 2 ,…,x n ,x n+1 – наименьшие неотрицательные вычеты этих решений. Тогда, очевидно, многочлен f(x) представим в виде:

f(x)=a(x-x 1 )(x-x 2 )…(x-x n -2)(x-x n-1 )(x-x n )+
+b(x-x 1 )(x-x 2 )…(x-x n -2)(x-x n-1 )+
+c(x-x 1 )(x-x 2 )…(x-x n -2)+
+…+
+ k(x-x 1 )(x-x 2 )+
+l(x-x 1 )+
+m.

Действительно, коэффициент b нужно взять равным коэффициенту при x n-1 в разности f(x)-a(x-x 1 )(x-x 2 )…(x-x n ) ;
коэффициент с – это коэффициент перед x n-2 в разности f(x)-a(x-x 1 )(x-x 2 )…(x-x n )- b(x-x 1 )(x-x 2 )…(x-x n-1 ) , и т.д.

Теперь положим последовательно x=x 1 ,x 2 ,…,x n ,x n+1 . Имеем:
1) f(x 1 )=m є 0(mod p) , следовательно, р делит m .
2) f(x 2 )=m+l(x 2 -x 1 ) є l(x 2 -x 1 ) є 0(mod p) , следовательно, р делит l , ибо р не может делить x 2 -x 1 , так как x 2 <p, x 1 <p .
3) f(x 3 ) є k(x 3 -x 1 )(x 3 -x 2 ) є 0(mod p) , следовательно, р делит k .
И т.д.

Получается, что все коэффициенты a, b, c,...,k, l кратны р . Это означает, что все коэффициенты a,a 1 ,…,a n тоже кратны р , ведь они являются суммами чисел, кратных р . ( Убедитесь в этом самостоятельно, раскрыв скобки в написанном выше разложении многочлена f(x) на суммы произведений линейных множителей.)

Ё

Прошу обратить внимание на важность условия простоты модуля сравнения в формулировке леммы 2 . Если модуль- число составное, то сравнение n -ой степени может иметь и более n решений, при этом, коэффициенты многочлена не обязаны быть кратными р . Пример: сравнение второй степени x 2 є 1(mod 16) имеет аж целых четыре различных решения (проверьте!):

x є 1(mod 16), x є 7(mod 16), x є 9(mod 16) , x є 15(mod 16).

Подведем итог.

Всякое нетривиальное сравнение по mod p равносильно сравнению степени не выше p-1 и имеет не более p-1 решений.

Наступил момент, когда наших знаний стало достаточно, чтобы легко понять доказательство еще одной замечательной теоремы теории чисел – теоремы Вильсона. Александр Вильсон (1714–1786) – шотландский астроном и математик-любитель, трудился профессором астрономии в Глазго. Теоремы Ферма, Эйлера и Вильсона всегда идут сладкой троечкой во всех учебниках и теоретико-числовых курсах.

Теорема (Вильсон). Сравнение , (p-1)!+1 є 0(mod p) выполняется тогда и только тогда, когда р - простое число.

Доказательство. Пусть р - простое число. Если р=2 , то, очевидно, 1!+1 є 0(mod 2) . Если р>2 , то рассмотрим сравнение:

[(x-1)(x-2)…(x-(p-1))]-(x p-1 -1) є 0(mod p) .

Ясно, что это сравнение степени не выше р-2 , но оно имеет р-1 решение: 1, 2, 3, ... , р-1 , т.к. при подстановке любого из этих чисел, слагаемое в квадратных скобках обращается в ноль, а (x p-1 ) сравнимо с нулем по теореме Ферма ( х и р взаимно просты, т.к. х<р ). Это означает, по лемме 2, что все коэффициенты выписанного сравнения кратны р , в частности, на р делится его свободный член, равный 1 Ч 2 Ч 3 Ч ... Ч (р–1)+1 .

Так как коэффициенты многочлена являются значениями симметрических многочленов от его корней, то здесь наметился путь для доказательства огромного числа сравнений для симметрических многочленов. Однако, я по этому пути дальше не пойду, оставляя это прекрасное развлечение читателю, которому нечем коротать долгие зимние вечера.

Обратно. Если р – не простое, то найдется делитель d числа р , 1<d<p . Тогда (р–1)! делится на d , поэтому (р–1)!+1 не может делится на d и, значит, не может делиться также и на р . Следовательно, сравнение , (p-1)!+1 є 0(mod 2) не выполняется.

Ё

Пример. 1 Ч 2 Ч 3 Ч ... Ч 10 + 1 = 3628800 +1 = 3628801 – делится на 11 (Вспомните признак делимости на 11- если сумма цифр в десятичной записи числа на четных позициях совпадает с суммой цифр на нечетных позициях, то число кратно 11).

Пример-задача. Доказать, что если простое число р представимо в виде 4n+1 , то существует такое число х , что х 2 +1 делится на р .

Решение. Пусть р=4n+1 – простое число. По теореме Вильсона, (4n)!+1 делится на р . Заменим в выражении 1 Ч 2 Ч 3 Ч ... Ч (4n)+1 все множители большие (p-1)/2=2n через разности числа р и чисел меньших (p-1)/2=2n . Получим:
(p-1)!+1 = 1 Ч 2 Ч 3 Ч … Ч 2n Ч (p-2n)(p-2n+1) Ч … Ч (p-1) = (1 Ч 2 Ч 3 Ч … Ч 2n)[A Ч p+(-1) 2n Ч 2n Ч (2n-1) Ч … Ч 2 Ч 1]+1 = A 1 p+(1 Ч 2 Ч 3 Ч … Ч 2n) 2 )+1 .

Так как это число делится на р , то и сумма (1 Ч 2 Ч 3 Ч … Ч 2n) 2 +1 делится на р , т.е. x=(2n)!=((p-1)/2)! .

Ё

Мелким шрифтом добавлю, что только что рассмотренный пример-задача, тесно связан с проблематикой, касающейся представления натуральных чисел в виде сумм степеней ( с показателями степени n>1 ) других натуральных чисел. Из нашего примера-задачи можно вывести, что натуральное число N в том и только в том случае представимо в виде суммы двух квадратов, когда в разложении N на простые множители все простые множители вида 4n+3 входят в четных степенях. Попробуйте самостоятельно доказать это утверждение в один из долгих зимних вечеров. Что касается представления чисел в виде сумм степеней, то здесь известна общая замечательная теорема:

Для любого натурального k существует такое натуральное N (разумеется, зависящее от k ), что каждое натуральное число представимо в виде суммы не более чем N слагаемых, являющихся k-ми степенями целых чисел.

У этой теоремы было известно несколько различных неэлементарных доказательств, но в 1942 году ленинградский математик Ю. В. Линник придумал чисто арифметическое элементарное доказательство, которое, однако, является исключительно сложным ( см., например, книжку А. Я. Хинчина "Три жемчужины теории чисел"). Что касается функции N(k ) , то здесь, в настоящее время почти ничего не ясно. Всякое натуральное число представимо в виде суммы четырех квадратов, девяти кубов (число 9 не может быть уменьшено), 21 штуки четвертых степеней (вот тут, кажется, что 21 может быть уменьшено до 19). Далее – полный туман. Всякое рациональное число представимо в виде суммы трех кубов рациональных чисел. * В качестве неплохого развлечения, предлагаю читателю следующую задачу: Доказать, что число 1 не может быть представлено в виде суммы двух кубов отличных от нуля рациональных чисел.

Задачки

1. Какому сравнению степени ниже 7 равносильно сравнение:
2x 17 + 6x 16 + x 14 + 5x 12 + 3x 11 + 2x 10 + x 9 + 5x 8 + 2x 7 + 3x 5 + 4x 4 + 6x 3 + 4x 2 + x + 4  є 0(mod 7).

2 . Используя процесс перебора всех вычетов из полной системы, решите сравнение
3x 14 + 4x 13 + 3x 12 + 2x 11 + x 9 + 2x 8 + 4x 7 + x 6 + 3x 4 + x 3 + 4x 2 + 2x є 0(mod 5)
предварительно понизив его степень.

3. Пусть (a 0 , m)=1. Укажите сравнение n -ой степени со старшим коэффициентом 1, равносильное сравнению
a 0 x n +a 1 x n-1 +...+a n є 0(mod m)

4. Докажите, что сравнение f(x) є 0(mod p), где р – простое, x n +a 1 x n-1 +...+a n-1 x+a n , n Ј p имеет n решений тогда и только тогда, когда все коэффициенты остатка от деления x p -x на f(x) кратны р .

5. Перед вами крупная задачка, разделенная на несколько мелких частей. Решите их по порядку:

- характеристическая функция множества простых чисел. Докажите, что

где, как обычно, [x] - целая часть числа х .

б) Сообразите, что

где p (m) – число простых чисел, не превосходящих m ("функция распределения" простых чисел).

в) Убедитесь, что

где:

("сигнум", т.е. знак х ).

г) Пусть p n - n -ое в порядке возрастания простое число, т.е. p 1 =2, p 2 =3, p 3 =5, ... Докажите, что p n Ј n 2 +1 для всех n .

д) Докажите, что (Внимание! Перед вами формула, выражающая простое число p n через его номер! ) ** :

NS НОВОСТИ

Бабка, дедка, внучка, жучка, кошка тянут за мышку, а курсор на экране не движется.

Наконец-то на Уралмаше занялись делом. Вместо шагающих эскаваторов налажен выпуск копающих.

* Доказательство этого утверждения впервые получено в 1825 году. Выглядит оно потрясающе: для рационального числа а непосредственно пишется его представление в виде суммы трех кубов рациональных чисел:

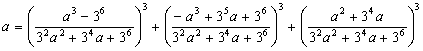
Совершенно неясно, как додуматься до такого доказательства.

** Вопреки распространенному мнению о "невозможности задать простые числа формулой", довольно легко сконструировать выражение n-ого простого числа через его номер. Беда в том, что от подобных формул мало толку. Во-первых, вычисление по ним не короче вычисления при помощи решета Эратосфена, во-вторых, эти формулы отнюдь не облегчают исследование различных закономерностей, связанных с простыми числами (распределение простых чисел, наличие в множестве простых чисел арифметических прогрессий заданной длины и т.п.).