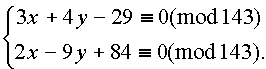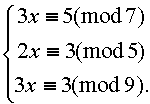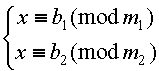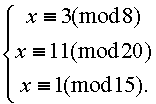§4. Теория сравнений

---

Вступление к следующим трем пунктам.

В следующих трех довольно скучноватых пунктах мы с вами будем рассматривать и учиться решать сравнения с одним неизвестным вида:

f(x) є 0(mod m) ,

где f(x)=a ₀ x ⁿ +a ₁ x ^n-1 +...+a _n-1 x+a _n – многочлен с целыми коэффициентами. Если m не делит a ₀ , то говорят, что n – степень сравнения. Ясно, что если какое-нибудь число х подходит в сравнение, то в это же сравнение подойдет и любое другое число, сравнимое с х по mod m . Запомните хорошенько (спрошу на экзамене!):

Решить сравнение – значит найти все те х , которые удовлетворяют данному сравнению, при этом весь класс чисел по mod m считается за одно решение.

Таким образом, число решений сравнения есть число вычетов из полной системы, которые этому сравнению удовлетворяют.

Пример. Дано сравнение: x ⁵ +x+1 є 0(mod 7)

Из чисел: 0, 1, 2, 3, 4, 5, 6, этому сравнению удовлетворяют два: x ₁ =2, x ₂ =4. Это означает, что у данного сравнения два решения:

x є 2(mod 7) и x є 4(mod 7) .

Сравнения называются равносильными, если они имеют одинаковые решения – полная аналогия с понятием равносильности уравнений. Однако (забегая вперед, открою приятный секрет), в отличие от алгебраических уравнений, которые частенько неразрешимы в радикалах, сравнение любой степени всегда решается, хотя бы, например, перебором всех вычетов по mod m . Правда, перебор и подстановка всех вычетов - зачастую весьма долгий процесс (особенно, при больших m и n ), но и здесь математики придумали хитроумные наборы инструкций, исполняя которые можно всегда найти все решения данного сравнения любой степени, минуя нудный процесс перебора.

Пункт 19. Сравнения первой степени.

В этом пункте детально рассмотрим только сравнения первой степени вида

ax є b(mod m),

оставив более высокие степени на съедение следующим пунктам. Как решать такое сравнение? Рассмотрим два случая.

Случай 1. Пусть а и m взаимно просты. Тогда несократимая дробь m/a сама просится разложиться в цепную дробь:

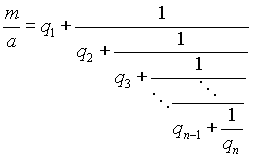
Эта цепная дробь, разумеется, конечна, так как m/a - рациональное число. Рассмотрим две ее последние подходящие дроби:

.

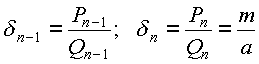Вспоминаем (пункт 9) важное свойство числителей и знаменателей подходящих дробей: mQ _n-1 -aP _n-1 =(-1) ⁿ . Далее (слагаемое mQ _n-1 , кратное m , можно выкинуть из левой части сравнения):

-aP _n-1 є (-1) ⁿ (mod m) т.е.

aP _n-1 є (-1) ^n-1 (mod m) т.е.

a[(-1) ^n-1 P _n-1 b] є b(mod m)

и единственное решение исходного сравнения есть:

x є (-1) ^n-1 P _n-1 b(mod m)

Ё

Пример. Решить сравнение 111x є 75(mod 322).

Решение. (111, 322)=1. Включаем алгоритм Евклида:

322=11 · 2+100

111=100 · 1+11

100=11 · 9+1

11=1 · 11

(В равенствах подчеркнуты неполные частные.) Значит, n=4 , а соответствующая цепная дробь такова:

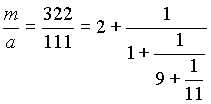
Посчитаем числители подходящих дробей, составив для этого стандартную таблицу:

	0	2	1	9	11
P n	1	2	3	29	322

Числитель предпоследней подходящей дроби равен 29, следовательно, готовая формула дает ответ: x є (-1) ³ Ч 29 Ч 75 є -2175 є 79(mod 322)

Ё

Ох уж эти мне теоретико-числовые рассуждения из разных учебников, продиктованные традицией изложения и необходимостью обязательно использовать ранее изложенную теорию! О чем идет речь в нескольких строках выше? Дано сравнение ax є b(mod m) , где a и m взаимно просты. Ну возьмите вы алгоритм Евклида, найдите те самые пресловутые u , v О Z такие, что au+vm=1 , умножьте это равенство на b : aub+vmb=b , откуда немедленно следует: aub є b(mod m) . Значит решением исходного сравнения является x є ub(mod m) . Собственно, и все. Поворчал.

Случай 2. Пусть (a,m)=d . В этом случае, для разрешимости сравнения ax є b(mod m) необходимо, чтобы d делило b , иначе сравнение вообще выполняться не может. Действительно, ax є b(mod m) бывает тогда, и только тогда, когда ax- b делится на m нацело, т.е. ax- b=t · m ,

t О Z , откуда b=ax- t Ч m , а правая часть последнего равенства кратна d .

Пусть b=db ₁ , a=da ₁ , m=dm ₁ . Тогда обе части сравнения xa ₁ d є b ₁ d(mod m ₁ d) и его модуль поделим на d :

xa ₁ є b ₁ (mod m ₁ ) ,

где уже а ₁ и m ₁ взаимно просты. Согласно случаю 1 этого пункта, такое сравнение имеет единственное решение x ₀ :

x є x ₀ (mod m ₁ )           (*)

По исходному модулю m , числа (*) образуют столько решений исходного сравнения, сколько чисел вида (*) содержится в полной системе вычетов: 0,1,2,..., m-2, m-1 . Очевидно, что из чисел x=x ₀ +t Ч m в полную систему наименьших неотрицательных вычетов попадают только x ₀ , x ₀ +m ₁ , x ₀ +2m ₁ , ..., x ₀ +(d-1)m ₁ , т.е. всего d чисел. Значит у исходного сравнения имеется d решений.

Подведем итог рассмотренных случаев в виде следующей теоремы

Теорема 1. Пусть (a,m)=d . Если b не делится на d , сравнение ax є b(mod m) не имеет решений. Если b кратно d , сравнение ax є b(mod m) имеет d штук решений.

Пример. Решить сравнение 111x є 75(mod 321) .

Решение. (111,321)=3 , поэтому поделим сравнение и его модуль на 3:

37x є 25(mod 107) и уже (37,107)=1 .

Включаем алгоритм Евклида (как обычно, подчеркнуты неполные частные):

107=37 Ч 2+33

37=33 Ч 1+4

33=4 Ч 8+1

4=1 Ч 4

Имеем n=4 и цепная дробь такова:

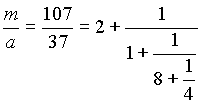
Таблица для нахождения числителей подходящих дробей:

q n	0	2	1	8	4
P n	1	2	3	26	107

Значит, x є (-1) ³ Ч 26 Ч 25 є -650(mod 107) є -8(mod 107) є 99(mod 107) .

Три решения исходного сравнения:

x є 99(mod 321), x є 206(mod 321), x є 313(mod 321) ,

и других решений нет.

Ё

А теперь я расскажу вам одну поучительную историю. Шли по российской дороге два мальчика. Один из них засмотрелся, упал ножками в открытый канализационный люк и, (О, боже!) – сломал ручку. Второй мальчик оказался хорошим товарищем – он вытащил упавшего мальчика, вытер его, подарил ему новую шариковую ручку и сказал: " Это тебя само провидение наказало за то, что ты всегда решал сравнения первой степени только одним способом. В следующий раз поступай осмотрительнее, – выбирай наилучшую дорогу".

Давайте и мы, чтобы не оказаться в неприятном виде перед своими товарищами, рассмотрим пару других способов решения сравнений первой степени. Эти способы излагаются дальше в виде теорем.

Теорема 2. Пусть m>1, (a,m)=1 Тогда сравнение ax є b(mod m) имеет решение: x є ba ^{j (m)-1} (mod m) .

Доказательство. По теореме Эйлера, имеем: a ^{j (m)} є 1(mod m) , следовательно, a Ч ba ^{j (m)-1} є b(mod m) .

Ё

Пример. Решить сравнение 7x є 3(mod 10) . Вычисляем:

j (10)=4; x є 3 Ч 7 ^4-1 (mod 10) є 1029(mod 10) є 9(mod 10) .

Видно, что этот способ решения сравнений хорош (в смысле минимума интеллектуальных затрат на его осуществление), но может потребовать возведения числа а в довольно большую степень, что довольно трудоемко. Для того, чтобы как следует это прочувствовать, возведите самостоятельно число 24789 в степень 46728.

Теорема 3. Пусть р – простое число, 0<a<p . Тогда сравнение ax є b(mod p) имеет решение:

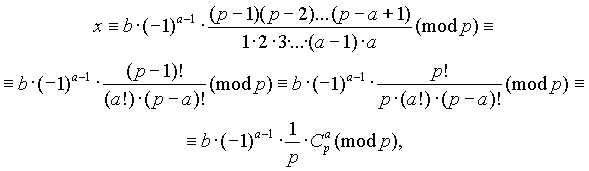
где C _a ^p – биномиальный коэффициент.

Доказательство непосредственно следует из очевидного сравнения

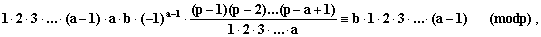
которое нужно почленно поделить на взаимно простое с модулем число 1 Ч 2 Ч 3 Ч ... Ч a-1 .

Ё

Пример. Решить сравнение 7x є 2(mod 11) . Вычисляем:

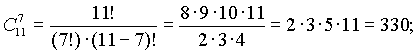
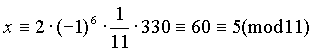
На этом пункт 19 можно было бы и закончить, но невозможно, говоря о решении сравнений первой степени, обойти стороной вопрос о решении систем сравнений первой степени. Дело в том, что умение решать простейшие системы сравнений не только является неотъемлемой частью общечеловеческой культуры, позволяющей гражданину не падать в ямы, расщелины и открытые люки. Такое умение, кроме всего прочего, пригодится нам при изучении сравнений произвольной степени, о которых пойдет речь в следующих пунктах.

Лемма 1 (Китайская теорема об остатках). Пусть дана простейшая система сравнений первой степени:

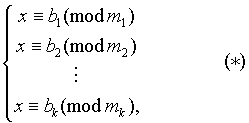
где m ₁ ,m ₂ ,...,m _k попарно взаимно просты. Пусть, далее, m ₁ m ₂ ...m _k =M _s m _s ; M _s M _s ^С є 1(mod m _s ) (Очевидно, что такое число M _s ^С всегда можно подобрать хотя бы с помощью алгоритма Евклида, т.к. (m _s ,M _s )=1 ); x ₀ =M ₁ M ₁ ^С b ₁ +M ₂ M ₂ ^С b ₂ +...+M _k M _k ^С b _k . Тогда система (*) равносильна одному сравнению

x є x ₀ (mod m ₁ m ₂ ...m _k ) ,

т.е. набор решений (*) совпадает с набором решений сравнения x є x ₀ (mod m ₁ m ₂ ...m _k ) .

Доказательство. Имеем: m _s делит M _j , при s № j. Следовательно, x ₀ є M _s M _s ^С b _s (mod m _s ) , откуда x ₀ є b _s (mod m _s ) . Это означает, что система (*) равносильна системе

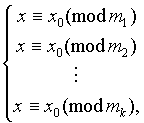
которая, очевидно, в свою очередь, равносильна одному сравнению x є x ₀ (mod m ₁ m ₂ ...m _k ) .

Ё

Пример. Однажды средний товарищ подошел к умному товарищу и попросил его найти число, которое при делении на 4 дает в остатке 1, при делении на 5 дает в остатке 3, а при делении на 7 дает в остатке 2. Сам средний товарищ искал такое число уже две недели. Умный товарищ тут же составил систему:

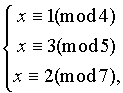
которую начал решать, пользуясь леммой 1. Вот его решение:

b ₁ =1 ; b ₂ =3 ; b ₃ =2 ; m ₁ m ₂ m ₃ , т.е. M ₁ =35, M ₂ =28, M ₃ =20 .

Далее он нашел:

35 Ч 3 є 1(mod 4)
28 Ч 2 є 1(mod 5)
20 Ч 6 є 1(mod 7)

т.е. M ₁ ^С =3, M ₂ ^С =2, M ₃ ^С =6. Значит x ₀ =35 Ч 3 Ч 1+28 Ч 2 Ч 3+20 Ч 6 Ч 2=513. После этого, по лемме 1, умный товарищ сразу получил ответ:

x є 513(mod 140) є 93(mod 140),

т.е. наименьшее положительное число, которое две недели искал средний товарищ, равно 93. Так умный товарищ в очередной раз помог среднему товарищу.

В следующей лемме, для краткости формулировки, сохранены обозначения леммы 1.

Лемма 2. Если b ₁ ,b ₂ ,...,b _k пробегают полные системы вычетов по модулям m ₁ ,m ₂ ,...,m _k соответственно, то x ₀ пробегает полную систему вычетов по модулю m ₁ m ₂ ...m _k .

Доказательство. Действительно, x ₀ =A ₁ b ₁ +A ₂ b ₂ +...+A _k b _k пробегает m ₁ m ₂ ...m _k различных значений. Покажем, что все они попарно не сравнимы по модулю m ₁ m ₂ ...m _k .

Ну пусть оказалось, что

A ₁ b ₁ +A ₂ b ₂ +...+A _k b _k є A ₁ b' ₁ +A ₂ b' ₂ +...+A _k b' _k (mod m ₁ m ₂ ...m _k ) .

Значит,

A ₁ b ₁ +A ₂ b ₂ +...+A _k b _k є A ₁ b' ₁ +A ₂ b' ₂ +...+A _k b' _k (mod m _s )

для каждого s , откуда

M _s M _s ^С b _s є M _s M _s ^С b' _s

Вспомним теперь, что M _s M _s ^С є 1(mod m _s ) , значит M _s M _s ^С є 1+m _s Ч t , откуда (M _s M _s ^С ,m _s )=1 . Разделив теперь обе части сравнения

M _s M _s ^С b _s є M _s M _s ^С b' _s

на число M _s M _s ^С , взаимно простое с модулем, получим, что b _s є b' _s (mod m _s ) , т.е. b _s =b' _s для каждого s .

Итак, x ₀ пробегает m ₁ m ₂ ...m _k различных значений, попарно не сравнимых по модулю m ₁ m ₂ ...m _k , т.е. полную систему вычетов.

Ё

Вот теперь пункт 19 с чистой совестью закончим.

Задачки

1. Reshite sravneniя: а) 5x є 3(mod 12); б) 256x є 179(mod 337); в) 1215x є 560(mod 2755); г) 1296x є 1105(mod 2413); д) 115x є 85(mod 335). 2 . Применив исконно русскую хитринку, решите систему сравнений 3 . Найдите все целые числа, которые при делении на 7 дают в остатке 3, при делении на 11 дают в остатке 5, а при делении на 13 дают в остатке 4 . 4 . Решите систему сравнений 5 . Пусть (m 1 ,m 2 )=d Докажите, что система сравнений имеет решения тогда и только тогда, когда b 1 є b 2 (mod d) . В случае, когда система разрешима, найдите ее решения . 6 . Решите систему сравнений 7 . Пусть (a,m)=1 , 1<a<m . Докажите, что разыскание решения сравнения ax є b(mod m) может быть сведено к разысканию решений сравнений вида b+mt є 0(mod p) , где р  – простой делитель числа а .