§ 3. Важнейшие функции в теории чисел

---

Пункт 15. z -функция Римана.

Этот пункт несколько сложнее предыдущих, так как для его понимания потребуются определенные знания из области математического анализа и теории функций комплексного переменного. Но было бы просто неправильно в параграфе под названием "Важнейшие функции в теории чисел" умолчать об одной из самых загадочных и влиятельных в математике функций - z -функции Римана, поэтому сделаем над собой некоторое усилие, отбросим внутреннюю скованность и попытаемся подойти к z -функции, чтобы познакомиться (надеюсь, более обстоятельно, чем с симпатичной девушкой, бегущей на автобус по суетливой улице). Всюду ниже буквой C обозначается поле комплексных чисел.

Определение. Пусть s О C , действительная часть Re( s ) > 1. z -функцией Римана называется функция комплексного переменного, задаваемая рядом:

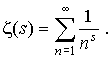
Правомерность такого определения подтверждает следующее наблюдение.

Наблюдение. В полуплоскости Re( s ) > 1 ряд
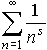сходится абсолютно.

Доказательство. Пусть s О C , Re( s ) > 1, s = s + i j (cм. рис. 5).

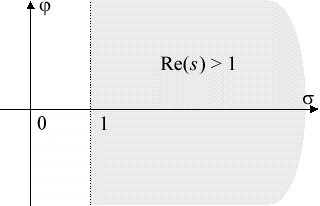
Рис. 5.

Посчитаем абсолютные величины членов ряда:

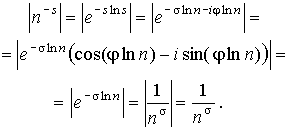
Теперь воспользуемся интегральным признаком сходимости (мы помним, что s > 1):

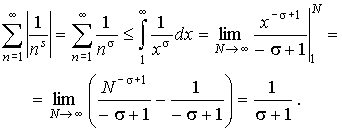
Значит, при s > 1 ряд
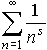сходится абсолютно.

Ё

Из этого наблюдения вытекает

Следствие 1. Функция z ( s ) аналитична в полуплоскости Re( s ) > 1.

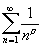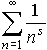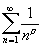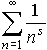Доказательство. Действительно, при всяком e > 0 и фиксированном r > 1+ e , числовой ряд мажорирует ряд из абсолютных величин = , где s і r , откуда, по теореме Вейерштрасса, следует равномерная сходимость ряда в полуплоскости Re( s ) і r . Сумма же равномерно сходящегося ряда из аналитических функций сама является аналитической функцией.

Теперь осталось только неограниченно приближаться к вертикальной пунктирной прямой Re( s ) = 1 на рис.5, устремляя e к нулю. Получается, что во всех полуплоскостях, граница которых сколь угодно близко подходит к прямой Re( s ) = 1, ряд 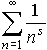сходится абсолютно и равномерно (почти как лошади на водопой), а его сумма - аналитическая функция.

Ё

Нематематическое (значит, лирическое) отступление.

Справедливости ради следует сказать, что функцию 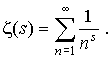впервые рассматривал Эйлер, который узнал много ее свойств и открыл свою знаменитую формулу 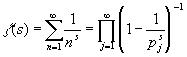, связывающую z ( s ) с простыми числами. Поэтому, правильнее было бы называть главную героиню этого пункта дзета-функцией Эйлера. Однако математики - люди твердолобые, и раз уж так повелось, талдычат все: "дзета-функция Римана" да "дзета-функция Римана". (Ортодоксальные математики до сих пор, например, условия аналитичности Даламбера - Эйлера функции комплексного переменного называют условиями Коши - Римана.) Разумеется, Риман тоже изучал функцию z ( s ) и высказал про нее много интересного, но мы не будем осуждать здесь ортодоксальных математиков за неправильное именование функции z ( s ), ибо само по себе имя ярчайшей звезды математического небосклона Георга Фридриха Бернгарда Римана есть вечная награда для любой функции, а z ( s ) такой орден, несомненно, заслужила.

Несколько слов о Бернгарде Римане (1826 - 1866), человеке, который в очень большой степени определил лицо современной математики. Риман был сыном деревенского священника, учился в Геттингенском университете, где в 1851 году получил степень доктора, в 1854 году стал приват-доцентом, в 1859 году - профессором, переемником Дирихле на кафедре математики. Болезненный, он провел последние несколько месяцев жизни в Италии, где и умер в сорокалетнем возрасте. За свою короткую жизнь Риман опубликовал небольшое число работ, но каждая из них - настоящая жемчужина, открывающая новые и плодотворные области. Именно Риману мы обязаны введением в анализ топологических представлений, понятию римановой поверхности, определению интеграла Римана, исследованию гипергеометрических рядов и абелевых функций, и так далее, и так далее. Именно ему мы обязаны новому взгляду на геометрию, при котором пространство вводится как топологическое многообразие с метрикой, задаваемой произвольной квадратичной дифференциальной формой (теперь мы говорим - римановы пространства). В работе 1859 года он исследовал количество простых чисел, меньших заданного числа, и дал точную формулу для нахождения этого числа с участием функции z ( s ). В этой знаменитой работе сформулирована не менее знаменитая "Гипотеза Римана" о нулях аналитического продолжения z ( s ) на всю комплексную плоскость (Верно ли, что все не действительные нули дзета-функции лежат на прямой Re( s ) =1/2?). Эта гипотеза, пожалуй, является одной из самых старых, трудных и насущных математических проблем. Она до сих пор не доказана и не опровергнута. Слава Богу, что ее формулировка неэлементарна, а то многочисленные доморощенные математики-ферматисты кинулись бы ее доказывать и одному из сотрудников математико-механического факультета Уральского госуниверситета пришлось бы, наряду с патологическими доказательствами теоремы Ферма, читать еще и "доказательства" гипотезы Римана, а это было бы уже совершенно невыносимо, так как может спровоцировать у сотрудника поступки суицидального характера.

Далее нам потребуются некоторые сведения из матанализа и теории функций комплексного переменного про бесконечные произведения. Бесконечные произведения - забавная и полезная потеха, которой почему-то, в отличие от бесконечных сумм, на лекциях в университете уделяют мало внимания. Исправим, отчасти, сие недоразумение.

Определение. Пусть u ₁ , u ₂ ,..., u _n ,... - бесконечная последовательность комплексных чисел и все u _j № - 1. Выражение вида:

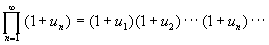( Є )

называется бесконечным произведением, а выражения:

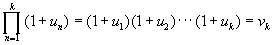
- частичными произведениями бесконечного произведения ( Є ).

Если последовательность частичных произведений v _k при k ® Ґ сходится к числу v № 0, то говорят, что бесконечное произведение ( Є ) сходится и равно v . В противном случае, если v _k не сходится (или v _{k ®} 0), то говорят, что бесконечное произведение ( Є ) расходится (соответственно, расходится к нулю).

Честно говоря, при первом знакомстве, словосочетание "расходится к нулю" вызвало у меня недоумение. Однако, при дальнейшем изучении конструкции бесконечного произведения, это недоумение рассеялось, так как выделение особого случая v _{k ®} 0 связано с традицией логарифмировать бесконечные произведения, чтобы перейти к рядам - более знакомым объектам, а логарифм нуля не имеет смысла и, видимо, находится далеко за пределами нашего разумения.

Теорема 1 (Признак сходимости ( Є )). Если ряд

u ₁ + u ₂ +... + u _n +...

сходится абсолютно, то бесконечное произведение ( Є ) сходится.

Доказательство . Пусть 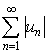- сходится, значит общий член этого ряда стремится к нулю и можно считать, что, например, | u _n | Ј 1/2 для всех n > n _{0 О} N . Пусть сначала u _{n О} R . Тогда, в силу замечательного предела 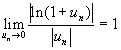, начиная с некоторого номера n > n ₀ , имеем: |ln (1 + u _n )| Ј 2| u _n |. Значит последовательность логарифмов частичных произведений

Sn = ln (1 + u ₁ ) + ln (1 + u ₂ ) +…+ ln (1 + u _n ) = ln v _n

сходится, т.к. 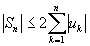, а справа в последнем неравенстве стоят частичные суммы сходящегося ряда. Следовательно, сходится и бесконечное произведение ( Є ).

Пусть теперь u _n - произвольные комплексные числа. Надо доказать, что при n ® Ґ сходятся две последовательности действительных чисел:

| v _n | = |(1+ u ₁ ) ·...· (1+ u _n )| = |1+ u ₁ | ·...· |1+ u _n | (1)

arg v _n = arg ((1+ u ₁ ) ·...· (1+ u _n )) = arg (1+ u ₁ ) +...+ arg (1+ u _n ) (2)

Пусть u _n = a _n + i b _n . Ясно, что для сходимости последовательности

| v _n | необходимо и достаточно сходимости последовательности | v _n | ² .

Но |1+ u _n | ² = |1 + a _n + i b _n | ² = 1 + a _n ² + b _n ² + 2 a _n и, так как

| a _n ² + b _n ² + 2 a _n | Ј | u _n | ² + 2| u _n |, то сходимость (1) следует из уже доказанного. Сходимость (2) следует из того, что при всех n , больших некоторого n ₀ , | arg (1+ u _n )| = 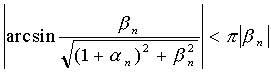(здесь опять использован замечательный предел
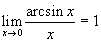), а | b _n | ® 0 т.к. u _n ® 0.

Ё

Ключ к пониманию огромной роли функции z ( s ) в теории чисел кроется в уже упоминавшейся выше замечательной формуле Эйлера.

Теорема 2 (Формула Эйлера).

,

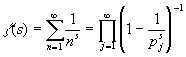где p _j - j -ое простое число и, таким образом, бесконечное произведение справа берется по всем простым числам.

Доказательство. Пусть X і 1, Re( s ) > 1. Ряды

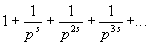
абсолютно сходятся (ибо мажорируются геометрическими прогрессиями). По теореме 1 это значит, что бесконечное произведение в формуле Эйлера сходится. Имеем (значок означает произведение по всем простым числам, не превосходящим X ):

.

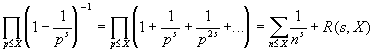Здесь при получении первого равенства использовалась формула суммы геометрической прогрессии, при получении последнего равенства существенную роль сыграла основная теорема арифметики. Через R ( s, X ) обозначен остаточный член, приписывание которого в нужном месте, вообще-то, позволяет поставить знак равенства между любыми величинами. На самом же деле, R ( s, X ) содержит бесконечное число слагаемых вида 1/ n ^s , не вошедших в стоящую перед ним сумму. Оценим остаточный член:

,

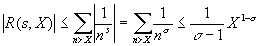т.е. R ( s, X ) ® 0, при X ® Ґ . Это и означает справедливость формулы Эйлера.

Ё

Следствие 2. При Re( s ) > 1, z ( s ) не имеет нулей.

Доказательство. Имеем:

,

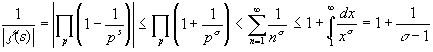значит,
.

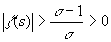Ё

Продолжим z ( s ) в полуплоскость Re( s ) > 0. Следующие лемма и следствие из нее призваны лишь показать один из возможных способов реализации такого продолжения, поэтому их доказательство можно пропустить без всякого ущерба для дальнейшего понимания.

Лемма 1. При Re( s ) > 0, N і 1

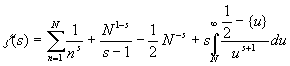
Доказательство. Имеем при Re( s ) > 1:

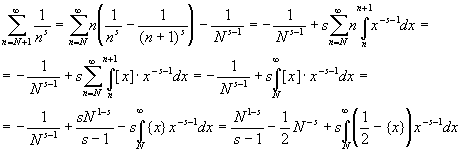
Но последний интеграл справа определяет аналитическую функцию даже при Re( s ) > 0. Поэтому, в силу принципа аналитического продолжения, утверждение леммы 1 справедливо.

Ё

Следствие 3. Функция z ( s ) является аналитической в полуплоскости Re(s)>0 за исключением точки s = 1; в точке s = 1 дзета-функция имеет простой полюс с вычетом, равным 1.

Ё

Оказывается, что дзета-функция имеет бесконечно много нулей в "критической полосе" 1 > Re( s ) > 0. Известно, что эти нули лежат симметрично относительно прямых Re( s ) =1/2 и Im( s ) = 0; известно, что в области Re( s ) і 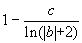, где b = Im( s ), а с - абсолютная постоянная, нулей у z ( s ) нет (Теорема Ш. Валле-Пуссена). Однако знаменитая гипотеза Римана о том, что все нули z ( s ) лежат на прямой Re( s ) = 1/2 до сих пор не доказана, хотя проверена для более 7 миллионов корней. Хотите посмотреть на первые десять корней z ( s ) = 0? Вот они:

r_1,2=1/2±14,134725i,
r_3,4=1/2±21,022040i,
r_5,6=1/2±25,010856i,
r_7,8=1/2±30,424878i,
r_9,10=1/2±32,935057i.

(Шутка: предлагаю непосредственной подстановкой убедиться, что это - корни z ( s ) = 0.)

Приведу еще, в качестве красивой картинки, без комментариев, ту самую удивительную формулу Римана, о которой уже упоминалось в этом пункте мелким шрифтом, для числа p ( x ) простых чисел, не превосходящих x :

,

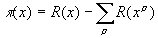где суммирование справа ведется по всем нулям z ( s ), а

.

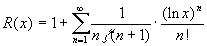К сожалению, рассказ о серьезных и нетривиальных применениях дзета-функции Римана выходит за рамки этой скромной книжки, поэтому, чтобы хоть как-то представить всю мощь этой функции, немного постреляем из пушки по воробьям - докажем с ее помощью пару известных утверждений.

Утверждение 1. Простых чисел бесконечно много.

Доказательство первое. Ну пусть p ₁ , p ₂ ,..., p _k - все простые. Тогда, так как

,

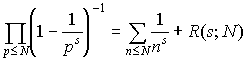получаем (при s = 1 и достаточно больших N ):

,

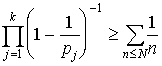ибо .
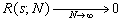Но это невозможно, ибо гармонический ряд
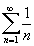расходится.

Ё

Доказательство второе. Ну пусть p ₁ , p ₂ ,..., p _k - все простые.

Тогда 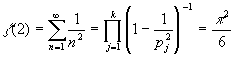, что невозможно, ибо конечное произведение суть рациональное число, чего никак не скажешь о числе p²/6.

Ё

Следующее утверждение гораздо менее известно, чем бесконечность множества простых. Возмем гармонический ряд 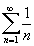и сильно проредим его, оставив в нем только слагаемые, обратные к простым числам и выкинув все слагаемые, являющиеся обратными к составным. Это действительно сильное прорежение, так как в натуральном ряде имеются сколь угодно длинные промежутки без простых чисел, например:

n ! + 2 , n ! + 3 , n !+4,..., n ! +n .

Гармонический ряд, как известно, расходится. Удивительно, что

Утверждение 2. Ряд 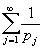из обратных величин ко всем простым числам расходится.

Доказательство. Пусть X О N . Имеем:

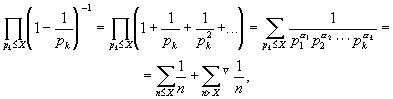
где значок С означает, что суммирование ведется по всем n>X, в разложении которых нет простых сомножителей, больших Х . Значит:

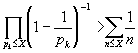
и ,

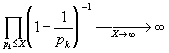так как гармонический ряд расходится. Из последнего вытекает, что бесконечное произведение

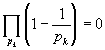
- расходится к нулю, т.е.

.

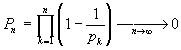Значит,

.

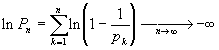Мы помним замечательный предел:

,

из которого следует, что:

,

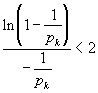откуда моментально:

.

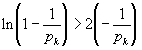Таким образом, в ряде

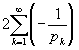
каждый член меньше соответствующего члена расходящегося к - Ґ ряда

,

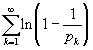следовательно, ряд
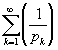расходится к + Ґ .

Ё

Справедливости ради отмечу: несмотря на то, что ряд 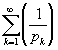самым невероятным образом расходится, он расходится все-таки медленнее гармонического. Про частичные суммы этих рядов известно, что 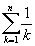растет как lnn^* , в то время, как
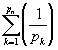растет только как ln(ln p _n ).

Позвольте мне быстренько закончить этот уже порядком поднадоевший пункт, а вместе с ним и весь третий параграф, установлением связи между дзета-функцией (которая не мультипликативна) и функцией Мебиуса m ( n ) (которая мультипликативна). Из этой связи понятно, что z ( s ) очень близка к мультипликативным функциям - просто единица, деленная на дзета-функцию, есть сумма (правда, бесконечная) мультипликативных функций.

Лемма 2. Пусть Re( s ) > 1. Тогда:

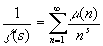
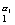Доказательство. Пусть n = p p 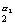· · · p 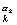. В лемме 1 из пункта 14 положим q (x)=1/x^s - мультипликативная функция. Тогда:

,

,

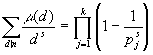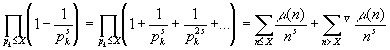где значок С , как и ранее означает, что суммирование ведется по всем n > X , в разложении которых нет простых сомножителей, больших Х . Далее, устремляя Х к бесконечности и вспоминая определение функции Мебиуса, получаем:

,

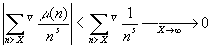следовательно:

.

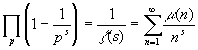Ё

Конечно, пункт 15 получился великоватым, поэтому на экзамене я не буду спрашивать его целиком - радуйтесь, ребятишки! Однако, если вы будете плохо себя вести: плеваться из трубочек на лекциях жеванными бумажками и тащить с пола в рот всякую гадость, то я спрошу на экзамене этот пункт целиком и, как следствие, поставлю двойку.

Завершим этим мажорным аккордом наше знакомство с дзета-функцией, а вместе с этим знакомством завершается и весь третий параграф. Ура!

Задачки

1. Сделайте что угодно, но вычислите z (3), после чего можно пойти погулять. 2 . Докажите, что ряд, составленный из обратных величин к простым числам, встречающимся в арифметической прогрессии 3, 7, 11, 15, 19, 23,..., расходится. 3 . Пусть L ( a ) = ln p для a = p l , где p - простое, l - натуральное; L ( a ) = 0 для остальных натуральных а** . Докажите, что при Re( s ) > 1 выполнено: . 4 . Пусть Re( s ) > 2. Докажите, что , где j ( n ) - функция Эйлера. 5 . Определим вероятность Р того, что k натуральных чисел x 1 , x 2 , …, x k будут взаимно простыми, как предел при N®Ґ вероятности P N того, что будут взаимно простыми k чисел x 1 , x 2 , …, x k , каждому из которых независимо от остальных присвоено одно из значений 1, 2,..., N , принимаемых за равновозможные.*** Докажите, что P=1/z(k).

NS	НОВОСТИ СПОРТА
Выдающееся мировое достижение установил пловец Сидоров - 100 метров за 4 секунды. Для достижения этого результата ему пришлось стартовать в верховьях Ниагарского водопада. Новый мировой рекорд установил Джон Бенсон в ходьбе на пять километров вольным стилем, превзойдя собственное же достижение почти на четыре километра.

 

* Более того, известен поразительный результат Л. Эйлера о том, что предел 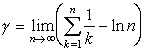существует и g»0,5772... . Число g называется теперь постоянной Эйлера.

**Функция L(a) называется функцией Мангольдта - весьма примечательный персонаж в теории чисел, знакомство с которым осталось, к сожалению, за рамками этой книжки.

***Сравните с определением, данным в пункте 3 этой книжки. Обратите внимание, что результат пункта 3 - теорема Чезаро - находится в прекрасном соответствии с утверждением этой задачи: P=6/p²=1/z(2).

Путь к решению этой весьма сложной задачи станет полегче, если вы докажете предварительно следующий факт:

Пусть k>1 и заданы системы x₁⁽¹⁾,x₂⁽¹⁾,...,x_k⁽¹⁾; x₁⁽²⁾,x₂⁽²⁾,...,x_k⁽²⁾; x₁⁽ⁿ⁾,x₂⁽ⁿ⁾,...,x_k⁽ⁿ⁾ целых чисел, не равных одновременно нулю. Пусть, далее, для этих систем однозначно определена некоторая (произвольная) функция f(x₁,x₂,x_k) . Тогда

,

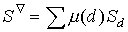где: m - функция Мебиуса, S^С обозначает сумму значений f(x₁,x₂,...x_k), распространенную на системы взаимно простых чисел, S_d обозначает сумму значений f(x₁,x₂,...x_k), распространенную на системы чисел, одновременно кратных d , а d пробегает натуральные числа.
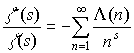
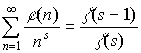