§ 3. Важнейшие функции в теории чисел
Пункт 14. Примеры мультипликативных функций.
Предыдущий пункт дал нам общие абстрактные знания о мультипликативных функциях вообще. Благодаря этому, в этом пункте мы сможем во всеоружии встретить целую серию примеров полезных мультипликативных функций. Большинство этих примеров строятся с использованием лемм предыдущего пункта, а в качестве исходного строительного материала берется какая-нибудь конкретная степенная функция q ( а ) = а s , которая, конечно, мультипликативна. Вы готовы? Начинаем.
Пример 1. Число делителей данного числа.
Пусть q ( а ) = а 0 є 1 - тождественная единица (заведомо мультипликативная функция). Тогда, если
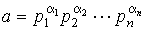 ,
,
то тождество леммы 1 пункта 13 принимает вид:
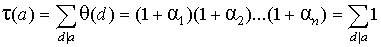 ,
,
- это не что иное, как количество делителей числа a . По лемме 2 пункта 13, количество делителей t ( a ) числа a есть мультипликативная функция.
Численный примерчик. t (720) = t (2 4 · 3 2 · 5) = (4 + 1)(2 + 1)(1 + 1) = 30.
Пример 2. Сумма делителей данного числа.
Пусть q ( a ) = a 1 є a - тождественная мультипликативная функция. Тогда, если
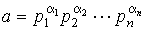 ,
,
то тождество леммы 1 пункта 13 принимает вид:
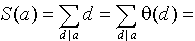
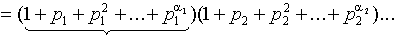
|
|
сумма первых (
a
+ 1) членов
геометрической прогрессии |
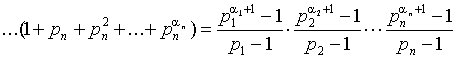
- сумма всех делителей числа a . По лемме 2 пункта 13, сумма всех делителей есть мультипликативная функция.
Численный примерчик.
| S (720) = S (2 4 · 3 2 · 5) = |
2
5
- 1
2 - 1 |
· |
3
3
- 1
3 - 1 |
· |
5
2
- 1
5 - 1 |
= 2418. |
Пример 3. Функция Мебиуса.
Функция Мебиуса m ( a ) - это мультипликативная функция, определяемая следующим образом: если p - простое число, то m ( p ) = -1; m ( p a ) = 0, при a > 1; на остальных натуральных числах функция доопределяется по мультипликативности.

Таким образом, если число a делится на квадрат натурального числа, отличный от единицы, то m ( a ) = 0; если же a = p 1 p 2· · · p n (теоретик-числовик сказал бы на своем жаргоне: "если a свободно от квадратов"), то m ( a ) = (-1) k , где k - число различных простых делителей a . Понятно, что m (1) = (-1) 0 = 1, как и должно быть.
Лемма 1. Пусть q ( a ) - произвольная мультипликативная функция,
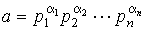 .
.
Тогда:
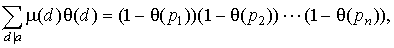
(при a = 1 считаем правую часть равной 1).
Доказательство. Рассмотрим функцию q 1 ( x ) = m ( x ) · q ( x ). Эта функция мультипликативна, как произведение мультипликативных функций. Для q 1 ( x ) имеем ( p - простое): q 1 ( p ) = - q ( x ); q 1 ( p a ) = 0, при a > 1. Следовательно, для q 1 ( x ) тождество леммы 1 пункта 13 выглядит так:
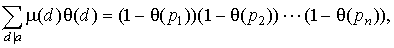
Ё

Следствие 1. Пусть q ( d ) = d -1 = 1/ d (это, конечно, мультипликативная функция),
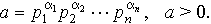
Тогда:
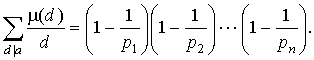
Воздержусь от доказательства этого следствия в силу банальности сего доказательства, но вот на правую часть этого тождества попрошу обратить внимание, так как она еще неоднократно у нас встретится. Физический смысл этой правой части раскрывает пример следующей функции.
Пример 4. Функция Эйлера.
Функция Эйлера, пожалуй, самая знаменитая и "дары приносящая" функция из всех функций, рассматриваемых в этом пункте. Функция Эйлера j ( a ) есть количество чисел из ряда 0, 1, 2,..., a - 1, взаимно простых с a . Полезность и практическое применение этой функции я продемонстрирую в следующих пунктах, а сейчас давайте поймем, как ее вычислять.

Лемма 2. Пусть
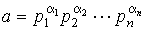 .
.
Тогда:
1)
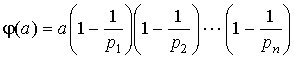 (формула Эйлера);
(формула Эйлера);
2)
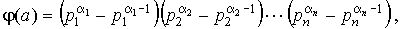
в частности, j ( p a ) = p a - p a -1 , j ( p ) = p - 1.
Доказательство. Пусть x пробегает числа 0, 1, 2,..., a - 1. Положим d x = ( x , a ) - наибольший общий делитель. Тогда j ( a ) есть число значений d x , равных 1. Придумаем такую функцию c ( d x ), чтобы она была единицей, когда d x единица, и была нулем в остальных случаях. Вот подходящая кандидатура:
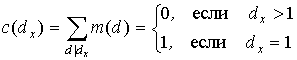
Последнее легко понять, если вспомнить лемму 1 из этого пункта и в ее формулировке взять q ( d ) є 1. Далее, сделав над собой некоторое усилие, можно усмотреть, что:
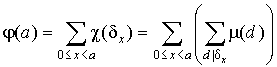
Поскольку справа сумма в скобках берется по всем делителям d числа d x = ( x , a ), то d делит x и d делит a . Значит в первой сумме справа в суммировании участвуют только те x , которые кратны d . Таких x среди чисел 0, 1, 2,..., a - 1 ровно a / d штук. Получается, что:
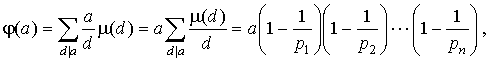
что и требовалось.
Пояснение для читателей, у которых предыдущие соображения не захотели укладываться в голову, например, из-за плохих погодных условий. Имеем

Зафиксируем некоторое d 0 такое, что d 0 делит a , d 0 делит x , x < a . Значит в сумме справа в скобках слагаемых m ( d 0 ) ровно a / d 0 штук и j ( a ) есть просто сумма
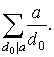
После этого, равенство
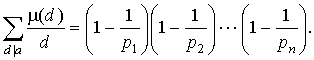
получается применением следствия из леммы 1 этого пункта. Должен признать, что приведенное доказательство формулы Эйлера и, в особенности, его последний момент с изменением порядка суммирования, объективно тяжеловаты для понимания. Но мы не боимся трудностей!
Второе утверждение леммы следует из первого внесением впереди стоящего множителя a внутрь скобок.
Ё
Оказывается, только что доказанная формула
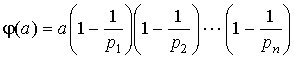
для вычисления функции Эйлера имеет ясный "физический смысл". Дело в том, что в ней отражено так называемое правило включений и исключений:
Правило включений и исключений. Пусть задано множество А и выделено k его подмножеств. Количество элементов множества А , которые не входят ни в одно из выделенный подмножеств, подсчитывается так: надо из общего числа элементов А вычесть количества элементов всех k подмножеств, прибавить количества элементов всех их попарных пересечений, вычесть количества элементов всех тройных пересечений, прибавить количества элементов всех пересечений по четыре и т.д. вплоть до пересечения всех k подмножеств.
Проиллюстрирую это правило на примере подсчета функции Эйлера для чисел вида
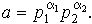
Посмотрите на рисунок 4.
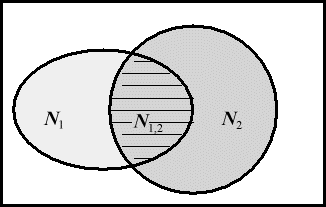
Рис. 4.
Прямоугольник изображает множество всех целых чисел от 0 до a ; овал N 1 - множество чисел, кратных p 1 ; кружок N 2 - числа, кратные p 2 ; пересечение N 1,2 - множество чисел, делящихся одновременно на p 1 и p 2 , т.е. на p 1 p 2 ; числа вне овала и кружочка взаимно просты с a . Для подсчета числа чисел, взаимно простых с a , нужно из a вычесть количество чисел в N 1 и количество чисел в N 2 (их, соответственно, a / p 1 и a / p 2 штук), при этом общая часть N 1,2 (там a /( p 1 p 2 ) штук чисел) вычтется дважды, значит ее надо один раз прибавить (вот оно, "включение - исключение"!). В результате получим:
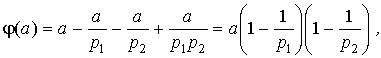
что я вам и утверждал. Мне кажется, что таким способом можно объяснить формулу Эйлера любому смышленому школьнику.
Кстати, любому смышленому школьнику вполне возможно объяснить и то, что при a > 2, j ( a ) всегда число четное. Действительно, если k взаимно просто с a и k < a , то число a - k тоже меньше a , взаимно просто с a и не равно k . (Если бы a и a - k имели общий делитель, то их разность a - ( a - k ) = k тоже делилась бы на этот делитель, что противоречит взаимной простоте a и k .) Значит числа, взаимно простые с a разбиваются на пары k и a - k , следовательно, их четное число.
Из леммы 2 вытекают приятные следствия.
Следствие 2. Функция Эйлера мультипликативна.
Доказательство. Имеем:
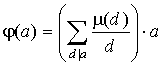
- произведение двух мультипликативных функций, первая из которых мультипликативна по лемме 2 пункта 13. Значит, j ( a ) - мультипликативна.
Ё
Следствие 3.
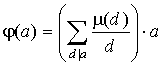 .
.
Доказательство. Пусть
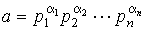 .
.
Тогда, по лемме 1 пункта 13 имеем:
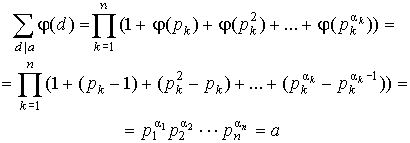 .
.
Ё
Численные примерчики.
j (5) = 5 - 1 = 4
j (30) = j (2 · 3 · 5) = (2 - 1)(3 - 1)(5 - 1) = 8
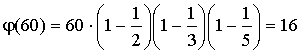
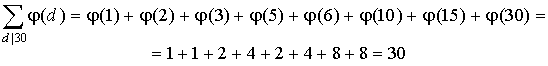
На этом, пожалуй, пункт 14 закончим. Кроме того, предложение, которое вы сейчас начали внимательно читать, тоже закончилось.
Задачки

|
1 . Потренируйтесь и найдите число делителей и сумму делителей чисел: а) 5600; б) 116424. 2 . Найдите сумму собственных делителей (т.е. делителей, отличных от самого числа) чисел: а) 6; б) 28; в) 496; г) 8128. Подивитесь полученному результату. * 3 . Составьте таблицу значений функции Мебиуса m ( n ) для всех значений n от 1 до 100. Бережно сохраните результат. 4 . Составьте таблицу значений функции Эйлера j ( n ) для всех значений n от 1 до 100. Бережно сохраните результат. 5 . Используя формулу Эйлера для j ( n ), еще раз докажите бесконечность множества простых чисел. 6 . Докажите, что существует бесконечно много чисел n О N , удовлетворяющих для всех k = 1, 2,..., n - 1 неравенствам
где S ( n ) - сумма всех делителей числа n . 7 . Докажите, что для любого натурального n выполняются неравенства
8 . На кафтане площадью 1 нашито 5 заплат, площадь каждой из которых не меньше 1/2. Докажите, что найдутся две заплаты, площадь общей части которых не меньше 1/5. 9 . Элитарный бизнес-клуб регулярно посещают 220 новых русских. При бизнес-клубе имеется шесть спортивных секций, представляющие следующие виды спорта: глазопучинг, разглядывание тяжестей, прыжки в ширину, дебилдинг, бег в трусцах, футбол ежом. В эти секции записались, соответственно, 30, 26, 32, 31, 28 и 36 человек. В несколько секций записались 53 новых русских, из них 24 братана посещают три или больше секций, 9 братанов не меньше четырех секций и 3 братана - даже пять секций. В последнюю тройку братанов входит один чудак, который записался во все шесть секций. Директор клуба хочет знать, сколько братанов не записались ни в одну секцию? 10 . Пусть k - натуральное число, d пробегает все делители числа а с условием j ( d ) = k . Докажите, что
11 . Пусть k - четное натуральное число, d пробегает все делители свободного от квадратов числа a = p 1 p 2· · · p k с условием 0 < d < Ц a . Докажите, что
|
* Числа равные сумме собственных делителей древние греки назвали совершенными. В формулировке задачи указаны первые четыре (известных еще Пифагору) совершенных числа. Евклид обнаружил, что если число 2 k -1 - простое, то число (2 k -1) · 2 k -1 обязано быть совершенным. Эйлер доказал, что все четные совершенные числа имеют такой вид. Неизвестно, существуют ли вообще нечетные совершенные числа; во всяком случае, такие числа должны быть больше 10 100 - результат хорошо организованной машинной проверки. Имеется ровно 24 значения k < 20000 , для которых число 2 k -1 - простое ( в этом случае k само обязано быть простым ). Простые числа вида 2 k -1 называются числами Мерсенна, по имени французского математика, который в 1644 году указал в большей части верный список всех таких простых, меньших 10 79 . Изрядно потрудившись, читатель сам может выписать наибольшее известное на сегодняшний день совершенное число, отталкиваясь от наибольшего известного на сегодня простого числа Мерсенна, указанного в пункте 6 этой книжки. Предполагается, что совершенные числа были известны уже в древнем Вавилоне и Египте, где рука с загнутым безымянным пальцем обозначала число шесть - первое совершенное число. Тем самым этот палец сам стал причастен к совершенству и за ним закрепилась привилегия носить обручальное кольцо.
| NS | НОВОСТИ НАУКИ |
|
Выпуск самых маленьких в мире шагающих экскаваторов наладила японская фирма "Сони". Экскаваторы бегают по полю в миниатюрных ботиночках и роют лунки для гольфа. "Ты моя суженная!" - сказал прямоугольник трапеции. Новости демографии. Завершилась перепись населения в Китае. Кончилась бумага. В лаборатории физики плазмы введен в действие уникальный реактор. В реактор загружены все необходимые реагенты и немного дрожжей. Через неделю физики будут отмечать окончание эксперимента. Новый компъютер разработан в институте физики металлов. Монолитный титановый монитор, стальной винчестер с затвором, хромель-алюмелевые кнопочки, отсутствие педалей и рулевой колонки делают новинку совершенно ненужной для грабителей. |
|