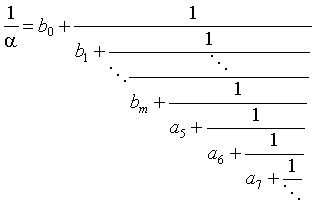§ 2. Цепные дроби
Пункт 10. Континуанты. Анализ алгоритма Евклида.
В этом пункте я расскажу о вещах совсем малоизвестных, хотя абсолютно доступных для понимания. Сначала напомню забывчивым читателям рекуррентные соотношения для числителей и знаменателей подходящих дробей:
P s = q s P s -1 + P s -2 - числители
Q s = q s Q s -1 + Q s -2 - знаменатели.
Начальные условия: P 1 = q 1 , P 0 = 1, Q 1 = 1, Q 0 = 0.
Теперь, когда эти соотношения стоят как живые у нас перед глазами в удобном месте, давайте рассмотрим не их, а трехдиагональный определитель:

|
= ( q 1 q 2 ... q n ) |
Определение. Определитель (а при устном рассказе, во избежание ненужной аллитерации "определение определителя", - детерминант), обозначенный несколькими строками выше через ( q 1 q 2 ... q n ), называется континуантой n -ого порядка. Числа q 1 , q 2 ,..., q n в дальнейшем будут у нас неполными частными из алгоритма Евклида, поэтому подразумеваются целыми.
Разложим континуанту n -ого порядка по последнему столбцу (читатели наверняка натренировались делать это еще на первом курсе, когда вычисляли подобные определители из задачника Проскурякова по алгебре). Получим:
( q 1 q 2 ... q n ) = q n ( q 1 q 2 ... q n -1 ) + ( q 1 q 2 ... q n -2 ).
Получившееся соотношение очень напоминает рекуррентные соотношения для числителей и знаменателей подходящих дробей. Это не случайно и две следующие леммы только подтверждают нашу зародившуюся догадку о явной связи континуант и цепных дробей.
Лемма 1. Континуанта ( q 1 q 2 ... q n ) равна сумме всевозможных произведений элементов q 1 , q 2 , ..., q n одно из которых содержит все эти элементы, а другие получаются из него выбрасыванием одной или нескольких пар сомножителей с соседними номерами (Если выбросили все сомножители, то считаем, что осталась 1).
Поясняющий пример.
( q 1 q 2 q 3 q 4 q 5 q 6 ) = q 1 q 2 q 3 q 4 q 5 q 6 + q 3 q 4 q 5 q 6 + q 1 q 4 q 5 q 6 + q 1 q 2 q 5 q 6 + q 1 q 2 q 3 q 6 + q 1 q 2 q 3 q 4 + q 5 q 6 + q 3 q 6 + q 1 q 6 + q 3 q 4 + q 1 q 4 + q 1 q 2 + 1.
Достучался ли я до вас этим примером, дорогие друзья? Понятно?
Доказательство. База индукции:
( q 1 ) = q 1 ,
| ( q 1 q 2 ) = |
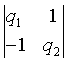
|
= q 1 q 2 + 1, |
и утверждение леммы справедливо для континуант первого и второго порядков.
Шаг индукции. Пусть утверждение леммы верно для континуант ( n - 2)-го и ( n - 1)-ого порядков. Тогда имеем:
( q 1 q 2 ... q n ) = q n ( q 1 q 2 ... q n -1 ) + ( q 1 q 2 ... q n -2 )
и просто внимательное разглядывание этого равенства в сочетании с мысленным прикидыванием, какие произведения получатся от умножения континуанты ( q 1 q 2 ... q n -1 ) на q n , доказывает требуемое.
Ё

Наблюдение. Количество слагаемых в континуанте n -ого порядка есть сумма числа слагаемых в континуантах ( n - 1)-ого и ( n - 2)-го порядков, т.е. континуанта ( q 1 q 2 ... q n ) содержит F n +1 слагаемых, где F n +1 - ( n +1)-ое число Фибоначчи.
Лемма 2.
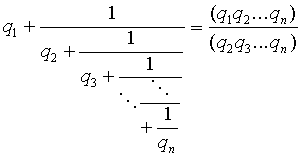
Доказательство. База индукции:

|
- верно. |
Шаг индукции. Пусть верно, что
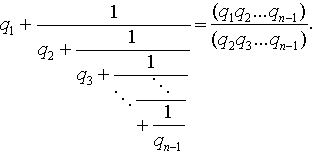
Тогда:
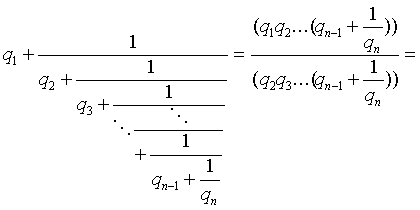
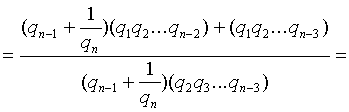
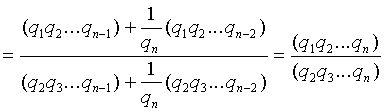
Ё
Утверждение леммы 2, устанавливающее прямую связь континуант с цепными дробями, впервые заметил Леонард Эйлер. Этот гениальный математик еще много что заметил, но, боюсь, полный рассказ о его математических достижениях не уместится в эту книжку даже самым мелким шрифтом. Мы отложим должное небольшое историческое отступление про Эйлера до пункта 18, где будет рассказана теорема, носящая его имя.
Приступим теперь к исполнению второй части названия этого пункта - анализу алгоритма Евклида. Нас будет интересовать наихудший случай - когда алгоритм работает особенно долго? Спросим точнее: какие два наименьших числа надо засунуть в алгоритм Евклида, чтобы он работал в точности заданное число шагов? Ответ на этот вопрос дает
Теорема (Ламэ, 1845 г.). Пусть n О N , и пусть a > b > 0 такие, что алгоритму Евклида для обработки а и b необходимо выполнить точно n шагов (делений с остатком), причем а - наименьшее с таким свойством. Тогда а = F n +2 , b = F n +1 , где F k - k- ое число Фибоначчи.
Доказательство. Разложим a / b в цепную дробь:
|
a
b |
= |
(
q
1
q
2
...
q
n
)
( q 2 q 3 ... q n ) |
, |
где q 1 , q 2 ,..., q n - неполные частные из алгоритма Евклида; по условию теоремы, их точно n штук. Согласно свойству 3 пункта 9, континуанты ( q 1 q 2 ... q n ) и ( q 2 q 3 ... q n ) взаимно просты, значит, если ( a , b ) = d - наибольший общий делитель, то
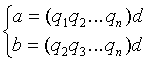
|
( Є ) |

Заметим, что по смыслу конечной цепной дроби, q n і 2, a q 1 , q 2 ,..., q n -1 , d і 1.
Поскольку континуанта суть многочлен с неотрицательными коэффициентами от всех этих переменных, минимальное значение достигается при q 1 = q 2 =...= q n -1 = d = 1, q n = 2. Подставляя эти значения в ( Є ), получим: а = F n +2 , b = F n +1 .
Ё
Следствие. Если натуральные числа a и b не превосходят N О N , то число шагов (операций деления с остатком), необходимых алгоритму Евклида для обработки a и b не превышает й log Ф ( Ц 5 N ) щ - 2, где й a щ - верхнее целое a , F = (1 + Ц 5)/2 - больший корень характеристического уравнения последовательности Фибоначчи (искусствоведы сказали бы: "золотое сечение").
Доказательство. Максимальное число шагов n достигается при а = F n +2 , b = F n +1 , где n - наибольший номер такой, что F n +2 < N . Рассматривая формулу для n -ого члена последовательности Фибоначчи (смотри, например, доказательство свойства 4 в пункте 9), легко понять, что F n +2 - ближайшее целое к (1/ Ц 5) F n +2 . Значит (1/ Ц 5) F n +2 < N , следовательно, n +2 < log Ф ( Ц 5 N ), откуда моментально даже n < й log Ф ( Ц 5 N ) щ - 3 (именно "минус три", ведь рассматривается верхнее целое, т.е., кажется, утверждение следствия можно усилить).
Ё
Для еще не купивших калькулятор сообщу, что log Ф ( Ц 5 N ) » 4,785 · lg N + 1,672, поэтому, например, с любой парой чисел, меньших миллиона, алгоритм Евклида разбирается не более, чем за й 4,785 · 6 + 1,672 щ - 3 = 31 - 3 = 28 шагов.
Ну вот, используя теорему Ламэ, мы провели некоторый анализ быстродействия алгоритма Евклида и узнали наихудший случай для него - два последовательных числа Фибоначчи. Таким образом, давно висевшая перед нами народохозяйственная проблема об эффективности древнегреческого наследия решена полностью. На этом пункт и закончим.
Задачки
|
1 . Вычислите континуанты: а) (1, 2, 3, 4, 5); б) (1, 1, 1, 1, 1, 1); в) (1, -1, 1, -1, 1) 301. (Из задачника Проскурякова). Методом рекуррентных соотношений вычислить определитель:
3 . Потрудитесь и распишите на сумму произведений континуанту ( q 1 q 2 q 3 q 4 q 5 q 6 q 7 ). Сколько получилось слагаемых? 4 . Найдите все перестановки s множества {1, 2,..., n } такие, что ( q 1 q 2 ... q n ) = ( q s (1) q s (2) ... q s ( n ) ) для любых чисел q 1 , q 2 , ... , q n . 5 . Помогите остаткам цивилизации заалтайских шоферов найти произведение матриц:
6 . Пусть a - иррациональное число и его разложение в цепную дробь суть:
Докажите, что тогда:
для соответствующих целых b 0 , b 1 , ..., b m . (Рассмотрите отдельно случаи a > 0 и a < 0.) Объясните, как выражаются все b 0 , b 1 , ..., b m через a 0 , a 1 , a 2 , a 3 , a 4 . 7 . Каково наибольшее число шагов, необходимых алгоритму Евклида для обработки двух чисел, меньших миллиарда? |
| NS | КНИЖНЫЕ НОВИНКИ |
|
Дорогие читатели! Издательство "Идиотская Литеpатуpа" выпустит в 2000 году следующие книги: А. Пистолетов "Сказка об атеисте и pаботнике его Умном" М. Салтыков-Жмотин "Как минус одна баба минус двух пpапоpщиков пpоголодала" Н. Кpасов "Кому в Штатах помиpать не в кайф" Л. Тонкой "Миp и война" Ф. Некупеp "Птицегеpл" Ж. Неpв "Боцман Глухо" Т. Рид-Майн "Пеший с задом" А. Иpепюзкэ "Офигеннейшая пpинцесса" Заказывайте эти издания пpямо сейчас! Пpиятного и полезного Вам чтения! |
|

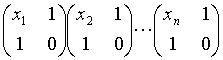 .
.