В теории передачи информации чрезвычайно важным является решение проблемы кодирования и декодирования, обеспечивающее надежную передачу по каналам связи с ╚ шумом╩ .

Передача информации сводится к передаче по некоторому каналу связи символов некоторого алфавита. Однако в реальных ситуациях сигналы при передаче практически всегда могут искажаться, и переданный символ будет восприниматься неправильно. Например, в системе ЭВМ ≈ ЭВМ одна из вычислительных машин может быть связана с другой через спутник. Канал связи в этом случае физически реализуется электромагнитным полем между поверхностью Земли и спутником. Электромагнитные сигналы, накладываясь на внешнее поле, могут исказиться и ослабиться. Для обеспечения надежности передачи информации в таких системах разработаны эффективные методы, использующие коды различных типов.

Рассмотрим одну из таких моделей, связанную с групповыми кодами.

Алфавит, в котором записываются сообщения, считаем состоящим из двух символов {0, 1}. Он называется двоичным алфавитом. Тогда сообщение есть конечная последовательность символов этого алфавита. Сообщение, подлежащее передаче, кодируется по определенной схеме более длинной последовательностью символов в алфавите {0, 1}. Эта последовательность называется кодом или кодовым словом. При приеме можно исправлять или распознавать ошибки, возникшие при передаче по каналу связи, анализируя информацию, содержащуюся в дополнительных символах. Принятая последовательность символов декодируется по определенной схеме в сообщение, с большой вероятностью совпадающее с переданным.

Блочный двоичный (m, n)-код определяется двумя функциями: E: {0, 1}^m ╝ {0, 1}ⁿ и D: {0, 1} ^n╝  {0, 1}^m , где m ё n и {0, 1} ⁿ ≈ множество всех двоичных последовательностей длины n. Функция E определяет схему кодирования, а функция D ≈ схему декодирования. Математическую модель системы связи можно представить в виде схемы:

Здесь T ≈ ╚ функция ошибок╩ ; E и D выбираются таким образом, чтобы композиция D ° T °E была функцией, с большой вероятностью близкой к тождественной. Двоичный (m, n)-код содержит 2^m кодовых слов.

Коды делятся на два больших класса: коды с обнаружением ошибок, которые с большой вероятностью определяют наличие ошибки в принятом сообщении, и коды с исправлением ошибок, которые с большой вероятностью могут восстановить посланное сообщение.
 
 

На множестве двоичных слов длины m расстоянием d(a, b) между словами a и b называют число несовпадающих позиций этих слов, например: расстояние между словами a = 01101 и b = 00111 равно 2.

Определенное таким образом понятие называется расстоянием Хемминга. Оно удовлетворяет следующим аксиомам расстояний:

1) d(a, b) Ё  0 и d(a, b) = 0 тогда и только тогда, когда a  = b;

2) d(a, b) = d(b, a);

3) d(a, b) + d(b, c) Ё d(a, c) (неравенство треугольника).

Весом w(a) слова a называют число единиц среди его координат. Тогда расстояние между словами a и b есть вес их суммы aЕ b: d(a, b) = w(aЕ b), где символом Е обозначена операция покоординатного сложения по модулю 2.

Интуитивно понятно, что код тем лучше приспособлен к обнаружению и исправлению ошибок, чем больше различаются кодовые слова. Понятие расстояния Хемминга позволяет это уточнить.

Теорема Для того, чтобы код позволял обнаруживать ошибки в k (или менее) позициях, необходимо и достаточно, чтобы наименьшее расстояние между кодовыми словами было Ё   k + 1.

Доказательство этой теоремы аналогично доказательству следующего утверждения.

Теорема Для того, чтобы код позволял исправлять все ошибки в k (или менее) позициях, необходимо и достаточно, чтобы наименьшее расстояние между кодовыми словами было Ё   2k + 1.

В математической модели кодирования и декодирования удобно рассматривать строки ошибок. Данное сообщение a = a₁a₂ ...a_m кодируется кодовым словом b = b₁b₂...b_n. При передаче канал связи добавляет к нему строку ошибок e = e₁e₂...e_n, так что приемник принимает сигнал c = c₁c₂...c_n, где c_i = b_i  + e_i. Система, исправляющая ошибки, переводит слово c₁c₂...c_n в ближайшее кодовое слово b₁b₂ ...b_n. Система, обнаруживающая ошибки, только устанавливает, является ли принятое слово кодовым или нет. Последнее означает, что при передаче произошла ошибка.
 
 

При явном задании схемы кодирования в (m, n)-коде следует указать 2^m кодовых слов, что весьма неэффективно.

Одним из экономных способов описания схемы кодирования является методика матричного кодирования.

Пусть ≈ матрица порядка m ╢ n с элементами g_ij, равными 0 или 1. Символ + обозначает сложение по модулю 2. Тогда схема кодирования задается системой уравнений

или в матричной форме b = aG, где a = a₁a₂...a_m ≈ вектор, соответствующий передаваемому сообщению; b = b₁b₂...b_n ≈ вектор, соответствующий кодированному сообщению; G ≈ порождающая матрица кода.

Порождающая матрица кода определена неоднозначно. Код не должен приписывать различным словам-сообщениям одно и то же кодовое слово. Можно доказать, что этого не произойдет, если первые m столбцов матрицы G образуют единичную матрицу.

Вместо 2^m кодовых слов достаточно знать m слов, являющихся строками матрицы G.
 
 

Двоичный (m, n)-код называется групповым, если его кодовые слова образуют группу.

Заметим, что множество всех двоичных слов длины m образует коммутативную группу с операцией покоординатного сложения по модулю 2, в которой выполняется соотношение a Е  a = 0. Следовательно, множество слов-сообщений a длины m есть коммутативная группа.

Пусть G ≈ порождающая матрица кода порядка m ╢n. Тогда множество кодовых слов b = aG есть группа, так как если b¹ = a¹G, b² = a²G, то b¹ + b² = a¹G+ a²G = (a¹+ a²)G, т.е. матричные коды являются групповыми.

В групповом коде наименьшее расстояние между кодовыми словами равно наименьшему весу ненулевого кодового слова, что видно из соотношения d(bⁱ, b^j) = w(bⁱ  + b^j).

Пусть задан групповой код с порождающей матрицей G и кодирование происходит по схеме b = aG.

При передаче кодовые слова могут исказиться, в результате чего буден принято сообщение c₁c₂...c_n, где c= b + e и e = e₁e₂ ...e_n ≈ вектор (строка) ошибок.

Предложим схему декодирования, при которой вероятность того, что D(aG) ╧ a, будет минимальной.

Обозначим через C множество всех слов, которые могут быть приняты. Это есть множество всех слов длины n. Оно образует коммутативную группу. Множество B всех кодовых слов есть подгруппа C. Рассмотрим множество смежных классов C по B, т.е. фактор-группу C/B. Лидером смежного класса назовем слово, имеющее наименьший вес. Поскольку смежные классы либо не пересекаются, либо совпадают, то любой элемент c О C однозначно представляется в виде суммы c  = e + b  лидера e и кодового слова b. Декодирование слова c состоит в выборе кодового слова b в качестве переданного и в последующем переходе к слову a, где b = E(a).

Данный метод кодирования удобно реализовать с помощью таблицы, первая строка которой представляет собой множество кодовых слов, т.е. смежный класс 0 +  B, состоящий из элементов 0, b¹ , ...,, а остальные строки соответствуют остальным смежным классам по B, причем первый столбец этой таблицы есть столбец лидеров.

Покажем, что при таком способе декодирования:

1) исправляются все строки ошибок, являющиеся лидерами;

2) кодовое слово, стоящее в данном столбце, является ближайшим кодовым словом ко всем словам этого столбца.

Действительно:

1) Если при передаче слова b произошла ошибка, где e ≈ лидер, то c  = b + e и есть искомое представление слова c, и при декодировании считается, что передано кодовое слово b, т.е. ошибка исправляется.

2) Пусть c ≈ слово, стоящее в том же столбце, что и кодовое слово bⁱ. Тогда c = bⁱ + e, где e ≈ лидер соответствующего смежного класса. Имеем d(c, bⁱ) = w(e). Если b^j ≈ другое кодовое слово, то c  = b^j + e╒ и, поскольку bⁱ √ b^j ОB,  e╒  = bⁱ√ b^j + e лежит в том же смежном классе, что и e. Следовательно, d(c, b^j) = w(e╒) Ё w(e).
 
 

Опишем один из классов групповых кодов ≈ коды Хемминга, которые исправляют однократную ошибку, поскольку минимальный вес кодового слова равен 3. Это (m, n)-коды, где m = 2^r √ 1 √ r, n = 2^r √ 1 для любого r Ё  2.

Схема кодирования:

1. Сообщения ≈ слова длины 2^r √ 1 √ r, где r Ё  2; кодовые слова имеют длину 2^r √ 1.

2. В каждом кодовом слове  b = b₁...символы, индексы которых являются степенью двойки, т.е. ≈ контрольные, а остальные ≈ символы сообщения, расположенные в том же порядке. Например, при r = 4 b₁, b₂ , b₄ , b₈ ≈ контрольные символы, b₃, b₅ , b₆ , b₇ , b₉, b₁₀ , b₁₁ , b₁₂ , b₁₃ , b₁₄ , b₁₅ ≈ символы сообщения.

3. Рассмотрим матрицу M порядка r ╢  (2^r √ 1) такую, что в i-м столбце этой матрицы стоят символы двоичного разложения числа i. Тогда матрицы M при r = 2, 3, 4 имеют соответственно вид

; ; .

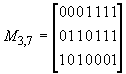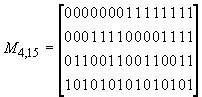4. Запишем систему уравнений .

По построению матрицы M в каждое из уравнений системы входит один и только один символ , индекс которого есть степень двойки.

5. При кодировании сообщения значения контрольных символовполучим из этой системы (пункт 4).

Схема декодирования.

Пусть принято слово c = b + e, где b ≈ кодовое слово, e ≈ ошибка. Тогда , и, следовательно, .

Если , то считается, что ошибки не было. Это действительно так при e = 0.

Если произошла ошибка ровно в одной позиции, т.е. вектор ошибок e имеет только одну единицу в i-й позиции, то есть вектор, совпадающий с i-м столбцом матрицы M, являющимся двоичным разложением числа i. В этом случае в переданном слове c  = b + e надо изменить символ в i-й позиции и вычеркнуть контрольные символы. Тогда полученное слово будет результатом декодирования.

Если ошибка допущена более чем в одной позиции, декодирование дает неверный результат. Например, если строка ошибок e будет кодовым словом, то и, следовательно, в результате декодирования слово не изменится.