Приложение 1.
Таблица значений функции ![]()
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
0.0 | 0.5000 | 5040 | 5080 | 5120 | 5160 | 5199 | 5239 | 5279 | 5319 | 5359 |
0.1 | 5398 | 5438 | 5478 | 5517 | 5557 | 5596 | 5636 | 5675 | 5714 | 5753 |
0.2 | 5793 | 5832 | 5871 | 5910 | 5948 | 5987 | 6026 | 6064 | 6103 | 6141 |
0.3 | 6179 | 6217 | 6255 | 6293 | 6331 | 6368 | 6406 | 6443 | 6480 | 6517 |
0.4 | 6554 | 6591 | 6628 | 6664 | 6700 | 6736 | 6772 | 6808 | 6844 | 6879 |
0.5 | 6915 | 6950 | 6985 | 7019 | 7054 | 7088 | 7123 | 7157 | 7190 | 7224 |
0.6 | 7257 | 7257 | 7291 | 7324 | 7357 | 7389 | 7422 | 7454 | 7486 | 7517 |
0.7 | 7580 | 7611 | 7642 | 7673 | 7704 | 7734 | 7764 | 7794 | 7823 | 7852 |
0.8 | 7881 | 7910 | 7939 | 7967 | 7995 | 8023 | 8051 | 8078 | 8106 | 8133 |
0.9 | 8159 | 8186 | 8212 | 8238 | 8264 | 8289 | 8315 | 8340 | 8365 | 8389 |
1.0 | 0.8413 | 8438 | 8461 | 8485 | 8508 | 8531 | 8554 | 8577 | 8599 | 8621 |
1.1 | 8643 | 8665 | 8686 | 8708 | 8729 | 8749 | 8770 | 8790 | 8810 | 8830 |
1.2 | 8849 | 8869 | 8888 | 8907 | 8925 | 8944 | 8962 | 8980 | 8997 | 9015 |
1.3 | 9032 | 9049 | 9066 | 9082 | 9099 | 9115 | 9131 | 9147 | 9162 | 9177 |
1.4 | 9192 | 9207 | 9222 | 9236 | 9251 | 9265 | 9279 | 9292 | 9306 | 9319 |
1.5 | 9332 | 9345 | 9357 | 9370 | 9382 | 9394 | 9406 | 9418 | 9429 | 9441 |
1.6 | 9452 | 9463 | 9474 | 9484 | 9495 | 9505 | 9515 | 9525 | 9535 | 9545 |
1.7 | 9554 | 9564 | 9573 | 9582 | 9591 | 9599 | 9608 | 9616 | 9625 | 9633 |
1.8 | 9641 | 9649 | 9656 | 9664 | 9671 | 9678 | 9686 | 9693 | 9699 | 9706 |
1.9 | 9713 | 9719 | 9726 | 9732 | 9738 | 9744 | 9750 | 9756 | 9761 | 9767 |
2.0 | 0.9772 | 9778 | 9783 | 9788 | 9793 | 9798 | 9803 | 9808 | 9812 | 9817 |
2.1 | 9821 | 9826 | 9830 | 9834 | 9838 | 9842 | 9846 | 9850 | 9854 | 9857 |
2.2 | 9861 | 9864 | 9868 | 9871 | 9875 | 9878 | 9881 | 9884 | 9887 | 9890 |
2.3 | 9893 | 9896 | 9898 | 9901 | 9904 | 9906 | 9909 | 9911 | 9913 | 9916 |
2.4 | 9918 | 9920 | 9922 | 9925 | 9927 | 9929 | 9931 | 9932 | 9934 | 9936 |
2.5 | 9938 | 9940 | 9941 | 9943 | 9945 | 9946 | 9948 | 9949 | 9951 | 9952 |
2.6 | 9953 | 9955 | 9956 | 9957 | 9959 | 9960 | 9961 | 9962 | 9963 | 9964 |
2.7 | 9965 | 9966 | 9967 | 9968 | 9969 | 9970 | 9971 | 9972 | 9973 | 9974 |
2.8 | 9974 | 9975 | 9976 | 9977 | 9977 | 9978 | 9979 | 9979 | 9980 | 9981 |
2.9 | 9981 | 9982 | 9982 | 9983 | 9984 | 9984 | 9985 | 9985 | 9986 | 9986 |
Приложение 2.
Взаимосвязь между распределениями вероятностей
Приложение 3.
![]() - распределение
- распределение
В таблице приведены значения (в процентах) квантилей ![]() в зависимости от числа степеней свободы m и вероятности a.
в зависимости от числа степеней свободы m и вероятности a.
Приложение 4.
Вывод формул (4.6) и (4.7).Пусть суммарные выплаты имеют сложное распределение Пуассона, т.е. ![]() ~
~![]() . Оценим число выплат, которое необходимо пронаблюдать. Обозначим через l среднее число выплат за каждый год, p1 и p2- среднее значение и второй момент величины индивидуальных выплат. Тогда среднее значение и дисперсия совокупных выплат за год задаются как lp1 и lp2. Предположим, что по рассматриваемой страховке имеются данные за n предыдущих лет, что дает агрегированную сумму выплат S. Нетто-взнос на предстоящий год есть lp1, а оценка, основанная лишь на предыдущих данных, есть S/n. Рассматривая S как случайную величину и используя нормальное приближение, имеем
. Оценим число выплат, которое необходимо пронаблюдать. Обозначим через l среднее число выплат за каждый год, p1 и p2- среднее значение и второй момент величины индивидуальных выплат. Тогда среднее значение и дисперсия совокупных выплат за год задаются как lp1 и lp2. Предположим, что по рассматриваемой страховке имеются данные за n предыдущих лет, что дает агрегированную сумму выплат S. Нетто-взнос на предстоящий год есть lp1, а оценка, основанная лишь на предыдущих данных, есть S/n. Рассматривая S как случайную величину и используя нормальное приближение, имеем
![]() ~
~![]()
Эти данные полностью
(k,p) - достоверны, если![]()
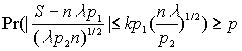
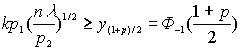
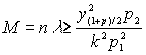
Получили формулу (4.6)
Пусть
m0 - математическое ожидание числа выплат для полной (k,p) - достоверности. Заменяя в (п. 4.1.) ln на m0, а неравенство на равенство получаем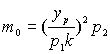 , (п. 4.2.)
, (п. 4.2.)
где yp - точка на единичном нормальном распределении, такая, что площадь между - yp и yp равна p.
Используя формулу достоверного взноса, имеем
![]()
Истинный нетто-взнос равен l
p1, а разность между ним и выражением (п. 4.3) равна:![]()
Рассмотрим первый член выражения (п. 4.4.) и выберем
Z таким образом , что![]()
для тех же
k и p, что и при определении m0. Поскольку![]() ~
~![]()
формула (п. 4.5.) означает, что
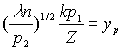
или
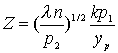
Записывая вместо l
n наблюдаемое число выплат M, а затем используя формулу (п. 4.2.) получаем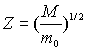
что и требовалось, поскольку молчаливо предполагалось, число
M £ m0.Замечание.
Поскольку обоснование выбора Z основывается лишь на одном из членов выражения (п. 4.4.), а член, включающий m игнорируется, поэтому Z определяется безотносительно к дополнительным данным.Приложение 5.
Оценка неизвестного параметра l в модели Пуассон-Гамма.
Предположим, что есть n наблюдений x1,x2,...,xnвеличины X, обозначим эти данные x. Байесовская оценка l по отклонению к функции квадратичных потерь есть
![]()
Апостериорная плотность вероятности l при заданном
x пропорциональна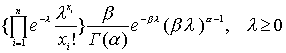
Здесь проигнорированы некоторые члены, не содержащие l
.Выражение (п. 5.1.) пропорционально
![]()
где
Можно показать, что апостериорное распределение l
есть гамма-распределение с параметрами![]()
что можно переписать как
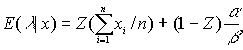
где
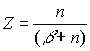 .
.Приложение 6.
Оценка неизвестных параметров в модели нормально-нормальное.
Предположим, что имеется n наблюдений X, т.е. x1,x2,...,xn, обозначим эти данные через x. Задача состоит в оценке E(x|q ) при заданном x. Используем байесовскую оценку по отношению к квадратичным отклонениям, то есть ![]() , что сводится к E[q |x], т.е. апостериорному среднему q при заданных x.
, что сводится к E[q |x], т.е. апостериорному среднему q при заданных x.
Апостериорная плотность вероятности q при заданном
x пропорциональна выражению:![]()
что, после алгебраических преобразований и игнорирования членов, не включающих q , оказывается пропорциональным
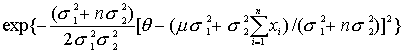
Из выражения (п.6.3) видно, что апостериорная распределения q при данном
x есть:![]() ~
~
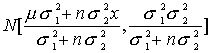 ,
,где
Следовательно,
![]()
что можно записать как
![]()
где
Приложение 7.
Вывод формулы достоверного взноса для эмпирической байесовской модели.
Найдем “наилучшую аппроксимацию” функции ![]() среди функций, линейных по наблюдаемым данным, т.е. среди функций
среди функций, линейных по наблюдаемым данным, т.е. среди функций
![]()
В силу симметричности модели по
Xj имеем![]()
Следовательно, необходимо рассмотреть лишь функции, имеющие вид
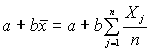
где
a и b - константы, которые следует определить. Для вычисления констант используется МНК, т.е. aи b находятся из минимизации выражения![]()
Форма, в которой будет решаться задача, такова: найти константы
aи b, минимизирующие выражение:![]()
Можно показать, что формулировки (п. 7.2.) и (п. 7.3.) эквивалентны. Сделать это можно следующим образом:
![]()
![]()
где
![]()
![]()
Заметим, теперь, что
E[AB] равно нулю, поскольку![]()
Используя тот факт, что все члены в
B - функция X, и![]()
![]()
Следовательно,
![]()
Член
A не содержит a или b, поэтому из формулы (п. 7.4.) ясно, что если aили b являются решением задачи (п. 7.3.), то они являются также решениями (п. 7.2.) и наоборот.Решение можно найти, дифференцируя математическое ожидание выражения (п. 7.3.) по
aи b и приравнивая обе частные производные к нулю![]()
![]()
откуда
![]()
![]()
Учитывая, что
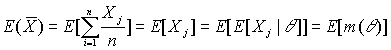
![]()
![]()
имеем
![]()
![]()
Если подставить эти формулы в выражение (п. 7.1.), записать
Z вместо b и отметить, что E[m(q )]есть нетто-взнос, который следует назначить при отсутствии предыдущих данных.Приложение 8.
Вывод формулы достоверного взноса в модели Бюльмана - Штрауба.
Достоверный взнос определяется как линейная функция наблюдений значений X, которая дает наилучшее приближение ![]() . Мы имеем дело с несимметричной моделью, так что рассматриваемые линейные функции наблюдаемых величин имеют вид:
. Мы имеем дело с несимметричной моделью, так что рассматриваемые линейные функции наблюдаемых величин имеют вид:
![]() (п. 8.1.)
(п. 8.1.)
Задача состоит в том, чтобы найти константы a1,a2,...,an, которые минимизируют
![]()
При помощи доводов, в точности повторяющих доказательство эквивалентности предположений (п. 7.2) и (п. 7.3), можно показать, что задача эквивалентна следующей: найти константы
a1,a2,...,an, которые минимизируют![]()
Решение этой задачи находится дифференцированием математического ожидания (п. 8.3) по
a1,...,an и приравниванием каждой из частных производных к нулю. Это дает следующие уравнения![]() (п. 8.4)
(п. 8.4)
![]()
Отмечая, что
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Можно свести предположения (п. 8.4) и (п. 8.5) к
![]()
![]()
Подставляя (п. 8.6) в (п. 8.7) получаем
![]()
Суммируя выражение (п. 8.8) для
k=1,2,...,n, видим, что![]()
Используя формулу (п. 8.9) в выражениях (п. 8.6), (п. 8.8), получаем
![]()
![]()
Подставляя выражения (п. 8.10) и (п. 8.11) в формулу (п. 8.1) получаем оценку нетто-взноса на единицу объема страхования:
![]()
что можно записать в более привлекательной форме как
![]()
где
![]()
![]()
Замечание. Если все
Pj равны, то достоверный взнос по модели 2 тот же, что и достоверный взнос по модели 1, если только заменить