Глава 6. Задача о разорении.
Рассмотрим состояние страхового портфеля не только в конце более длинных периодов времени (чем год), но и в промежуточные моменты времени, вне зависимости от того, предъявляются ли страховой компании требования о выплате. В частности, обсудим вопрос: имеются ли у компании достаточные средства для того, чтобы оплатить потенциальные требования о выплате?
Сумма, которую компания имеет в момент времени t, называется активами на момент t. Ясно, что
[Активы на момент t] = [Исходные активы] + [Взносы на момент t] - [Выплаты на момент t] (6.1)
Нашей целью будет определение вероятности разорения и ее зависимости от
Чтобы найти взаимосвязь предположим, что
Пусть
Предположим, что страховые взносы поступают непрерывно и с фиксированной скоростью
c. Тогда по (6.1) имеемU(t)=U+ct-S(t)
Ясно, что
{U(t)}t³ 0 - случайный процесс, называемый процессом изменения активов.Когда активы падают до нуля, то говорят, что произошло разорение страховщика.
Y (U) называется вероятностью окончательного разорения при данных начальных активах U:
Y (U)=Pr(u(t)<0, при некотором t, 0<t<¥ )
Введем дополнительные предположения:
а) случайные величины ![]() независимы и одинаково распределены (обозначим общую для всех Xi функцию распределения через F(x), плотность распределения через f(x));
независимы и одинаково распределены (обозначим общую для всех Xi функцию распределения через F(x), плотность распределения через f(x));
б) случайные величины
в) случайный процесс
![]()
Тогда процесс
{S(t)}t³ 0 является пуассоновским процессом.Обозначим
![]()
C можно записать в терминах относительной надбавки
![]()
Предположим, что
Mx(t) - производящая функция моментов для распределения страховых выплат.Обычно невероятно трудно вычислить точно вероятность (окончательного) разорения Y(U). Неравенство Лундберга дает некоторую верхнюю границу для Y(U)
Y (U) £exp(-RU
) (6.2)где
R - поправочный коэффициент;U - начальные активы.
Это неравенство имеет два преимущества над точным выражением для Y(U):
1) его просто применять;
2) если
U не слишком малы, то достигаемая аппроксимация очень хорошая.Неравенство (6.2) говорит о том, что вероятность разорения ограничена функцией, экспоненциально убывающей с ростом U. Вероятность разорения убывает с ростом U и R.
Поправочный коэффициент R является единственным положительным корнем уравнения
![]()
Уравнение (6.3) обычно решается численно (например, используется метод Ньютона).
Пример 6.1. Распределение выплат экспоненциально с функцией распределения
F(x)=1-exp(-a x), x>0. Найти поправочный коэффициент.Решение. Производящая функция моментов
M(t)=a /(a -t), а среднее p1=1/a, то нужно решить уравнение![]()
Тогда поправочный коэффициент равен
![]()
Если (6.3) решается с помощью численных методов, то верхняя граница для
R может оказаться очень полезной. Из (6.3) получаем![]()
![]()
откуда
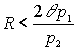
Зависимость поправочного коэффициента от надбавки безопасности представлена на рис 6.1.; первый график соответствует экспоненциальному распределению со средним 1, а второй - постоянному распределению страховых выплат (каждая страховая выплата имеет размер
1).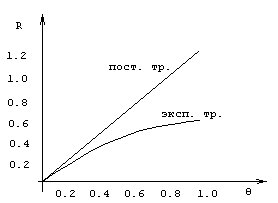
Рис 6.1. График зависимости
R от q.окончательного разорения в экспоненциальном случае.
В общем случае Y(U) удовлетворяет уравнению
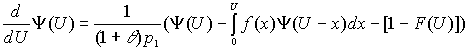
Это уравнение обычно решается с помощью численных методов. В случае экспоненциального распределения решением (6.5) является функция
![]()
Приведенное решение позволяет провести исследование неравенства Лундберга в экспоненциальном случае (см. рис 6.2)
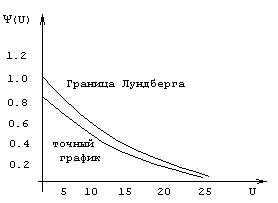
Рис 6.2. Графики Y
(U) и exp(-RU) в случае экспоненциальности страховых выплат со средним 1 и надбавкой безопасности q=0,2.На рисунке 6.3 показано, что вероятность разорения резко падает с увеличением надбавки безопасности.
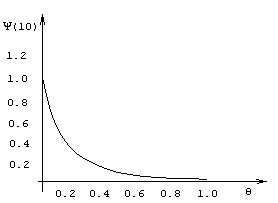
Рис 6.3. График зависимости Y
(10) от q в случае, когда выплаты распределены экспоненциально со средним 1.Согласно неравенству Лундберга (6.2), верхняя граница для вероятности окончательного разорения примет минимальное значение, если величина поправочного коэффициента максимальна. Изучим влияние эффекта перестрахования на поправочный коэффициент.
Рассмотрим эксцедентное перестрахование. Если X - размер страховой выплаты, M - уровень собственного удержания, то Y=min(X,M) - выплаты страховщика, Z=max(0,X-M) - выплаты перестраховщика. Обозначим через q и x надбавки безопасности страховщика и перестраховщика соответственно.
Из неравенства
q p1³x E(Z),
при q< x (6.6)можно найти нижний предел
M.Пример 6.2.
Страховые выплаты, производимые страховщиком, имеют экспоненциальное распределение со средним 1. Определить нижний предел M.Решение.
Математическое ожидание выплат, производимых перестраховщиком таково![]()
Из (6.6) получаем
![]()
Если q =0,15и x =0,3, то
M ³ln2 = 0.693.Условие (6.6) устанавливает предел, показывающий насколько большой может быть часть риска, передаваемая перестраховщику. Но какое значение
M должен выбрать страховщик? Поскольку q£x, перестрахование уменьшает ожидаемую прибыль страховщика. Перестрахование - это всегда компромисс между ожидаемыми прибылями и безопасностью. Цель перестрахования - повысить безопасность и безопасность достигается с помощью минимизации вероятности разорения, или максимизации поправочного коэффициента.С появлением перестрахования поправочный коэффициент удовлетворяет уравнению
![]()
Уравнение (6.7) практически имеет вид уравнения (6.3), в левой части берется во внимание появление уровня удержания, а правой - необходимость платить перестраховочный взнос.
В (6.7) следует выбирать
M так, чтобы R принял наибольшее значение.Пример 6.3. (продолжение примера 6.2) В случае, если
f(x)=e-x, x>0, (6.7) примет вид![]()
уравнение для определения
R. Выбираем M так, чтобы получить max R. Уравнение (6.8) можно решить числено, например, методом Ньютона.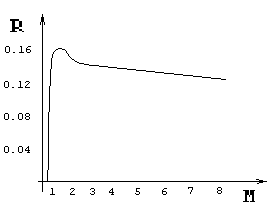
Рис 6.4. График зависимости поправочного коэффициента
R от уровня удержания M.Из рисунка 6.4. видно, что существует некоторое значение
M (близкое к 1,5 в нашем примере) такое, что если установить уровень удержания ниже этого значения, то вероятность разорения слишком велика - страховщик передает слишком много риска по слишком высокой цене. Если уровень удержания устанавливается выше указанного значения, то возможно небольшое уменьшение безопасности бизнеса или соответствующее увеличение ожидаемой прибыли.Задачи
№ Пункта | Рекомендуемые задачи |
6.1 | 6.1 |
6.4 | 6.2, 6.3, 6.4 |
6.5 | 6.5, 6.6 |
6.6 | 6.7, 6.8, 6.9, 6.10 |
6.1:
Втечение года произведено 6требований о выплате в рамках некоторогостраховогопортфеля. Дни, в которые эти требования были предъявлены и размеры требований указаны в таблице 6.1.Таблица
6.1.Дни, в которые были предъявлены требования о выплате, размеры страховых выплат и страховые взносы (в фунтах стерлингов)День | 47 | 99 | 199 | 286 | 306 | 358 |
Размер выплаты | 97 | 104 | 157 | 56 | 23 | 99 |
Компания располагает данными о прошлом поведении риска: число требований о выплате в предыдущие пять лет составляло
4, 3, 6, 2 и 5, а среднее значение страховой выплаты составляло£120. Компания исчисляет страховой взнос, используя25% надбавку безопасности q, основываясь на оценке годичных страховых выплат. Найдите совокупный годичный страховой взнос, предполагая, что страховые взносы уплачиваются непрерывно, а также постройте диаграмму процесса изменения активов.Прокомментируйте диаграмму и выбор q.
6.2.Предположим, что все страховые выплаты имеют один и тот же фиксированный размер k. Покажите, что поправочный коэффициент R удовлетворяет уравнению
ekR=1+(1+q )kR,
где R<2q /k (6.9)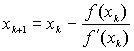 ,
,
где
x0 - некоторое начальное приближение к решению уравнения f(x)=0,в случае уравнения
(6.9) приобретает видR1=![]()
6.4.
а) Пример
6.1 дает общее решение для R в случае экспоненциального распределения. Вычислите R при (i ) a= 1 и (ii) a = 0.1.
6.5.
Предположим, что Р(x)= 1-exp(-0.05х).а) Подготовьте грубые графики, аналогичные изображенным на рисунке
6.2, дляq= 0.1 Каково (точное) значение U, для которого y(U)=0.05? Каково минимальное значениеU, начиная с которого разность exp(-RU)-y (U) становится меньше, чем 0.01?
6.6.
Предположим, что страховые выплаты имеют только два размера: 2/3 и 4/3, причем выплаты принимают указанные значения с одинаковой вероятностью. Пусть ещеq= 0.1.с) Сравните границы Лундберга для следующих трёх случаев: для случая, когда выплаты распределены экспоненциально со средним
1; для случая постоянных выплат, равных 1, для распределения выплат, указанного в условиях упражнения. Насколько далека точная вероятность разорения в экспоненциальном случае от указанных границ?6.7.
В примере 6.3 мы показали, что поправочный коэффициент удовлетворяет неравенству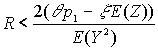 ,
,
где
Y - выплата, производимая страховщиком; Z- выплата, производимая перестраховщиком; а x - надбавка безопасности, установленная перестраховщиком.6.8. В условиях примера 6.4, покажите, что
![]()
и выведите из (6.27) неравенство
![]()
Рисунок 6.4 дает график этой верхней границы в зависимости от
M.6.9.Пополним кое-какими деталями пример 6.5. Покажите, что решение уравнения (6.25) эквивалентно решению уравнения
![]() ,
,
где
6.10. Предположим, что распределение страховых выплат - это U(0,20), т.е. f(x)=0.05, 0<x<20. Страховщик использует надбавку безопасности q=0.1, перестрахование осуществляется с надбавкой безопасности x =0.2. Пусть уровень удержания равен M. Покажите, что среднее выплаты Z, производимой перестраховщиком, составляет
![]()
Используйте (6.19) и (6.28) для того, чтобы показать
![]()
Каков минимальный уровень удержания?