Глава 5. Модели риска.
Рассмотрим портфель рисков, принимаемых на себя страховой компанией, скажем, на год. Сконцентрируем свое внимание на общем размере страховых выплат по этому портфелю.
В индивидуальных моделях требования о выплате изучается на уровне договора страхования. Затем требования выплат от индивидуальных полисов суммируются с целью нахождения совокупных требований выплат для всего портфеля полисов.
Предположим, что:
Тогда совокупное требование выплат
S из портфеля, составляет![]()
где
Yj есть объем требования от j-го риска, n - количество рисков.Тогда каждое
Yj~сложное биномиальное распределение с Nj~ B(1,qj), и![]()
![]()
Замечание.
Важным элементом индивидуальных моделей риска является допущение о том, что по каждому договору страхования возможно предъявление только одного требования о выплате. Эти модели в основном используются для описания портфеля договоров страхования жизни.
Рассмотрим два примера, показывающие, как используются формулы (5.1) и (5.2). Первый пример подводит к идее надбавки безопасности, в то время как второй показывает, каким образом компания может установить уровень собственного удержания.
Пример 5.1. Предположим, что имеется 300 независимых договоров страхования жизни, заключенных сроком на год. Страховая сумма составляет
£1000 по всем договорам страхования. Вероятность предъявления требования о выплате составляет 0.1 по некоторым 100 договорам страхования и 0.2 по 200 оставшимся. Определить относительную надбавку безопасности.Решение. Сначала отыщем среднее и дисперсию общего размера страховых выплат, используя (5.1) и (5.2)
![]()
![]()
Проводимая нами работа связана с определением страхового нетто-взноса, который до сих пор рассматривался нами равным ожидаемому размеру страховых выплат
E(Sn). Мы игнорировали как издержки, так и прибыль страховщика, а также риск, принимаемый на себя страховой компанией, заключающей договор страхования: общий размер страховых выплат, как показывает V(Sn), может превзойти ожидаемый размер требований о выплате. Простой путь вычисления необходимой надбавки к нетто-взносу - это потребовать, чтобы совокупный (новый) страховой взнос покрывал с определенной вероятностью (скажем, 95 процентов) ожидаемый общий размер страховых выплат (вместо того, чтобы пользоваться средним значением общего размера страховых выплат).Если предположить, что общий размер страховых выплат является случайной величиной, имеющей распределение, близкое к нормальному, то компания может установить совокупный страховой взнос на уровне
![]()
(Поскольку
E(S)=50000; s=6403; с вероятностью 0,95 стандартная нормальная случайная величина принимает значение £1,645).Сколько должен платить каждый страховщик? Кажется справедливым, чтобы доля каждого страховщика в совокупном страховом взносе была пропорциональна ожидаемой по договору с ним выплате. Таким образом, если среднее значение ожидаемой выплаты по договору с
i-м страхователем равно Mi, то чистый взнос должен составлять (1+q )Mi. Сумма qMi называется абсолютной надбавкой безопасности, а q называется относительной надбавкой безопасности.Общий размер взносов составит
![]()
В нашем случае
![]()
В общем случае относительная надбавка безопасности определяется так:
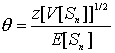
где
z - граница, соответствующая по стандартному нормальному распределению, выбранной доверительной вероятности p, т.е. если Y - стандартная нормальная случайная величина, тоПример 5.2.
Страховая компания заключила 8000 договоров страхования жизни сроком на год. Информация о страховых суммах приведена в таблице 5.1, в качестве единицы измерения страховой суммы выбрана сумма в £10 000.Таблица 5.1. Договоры страхования и страховые суммы
Размер страховых выплат | Число договоров |
1 | 5 000 |
2 | 3 000 |
Страхователи могут рассматриваться независимо друг от друга. Вероятность предъявления требования о выплате по каждому договору страхования равна 0,2. Определить уровень собственного удержания и стоимость перестрахования.
Решение. Сначала найдем среднее и дисперсию общего размера страховых выплат, используя (5.1) и (5.2)
![]()
![]()
Компания заинтересована в сохранении контроля над страховыми выплатами и пытается поэтому определить вероятность, с которой общий размер выплат превзойдет, например, 240 единиц. С помощью центральной предельной теоремы получаем, что
![]()
Компания может уменьшить эту вероятность, устанавливая уровень собственного удержания
M. Цена за перестрахование составляет 0,022 за £1 покрываемой суммы (т.е. пропорциональна ожидаемому размеру выплат).Предположим, что компанией установлен уровень удержания
M= £16 000. Найдем вероятность того, что общий размер страховых выплат (включая и перестраховочный взнос) превзойдет 240 единиц.Найдем новые среднее м дисперсию общего размера страховых выплат:
![]()
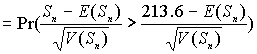
![]()
Вероятность того, что общие издержки компании превзойдут 240 единиц уменьшилась незначительно - с 0,14 до 0,13. Цена которую платит за это компания - это увеличение среднего значения издержек с 220 до 222,4. В среднем, прибыль компании уменьшится, но взамен компания приобретет некоторую защиту от неблагоприятного поведения требований о выплате.
В отличии от моделей индивидуальных рисков, модель коллективных рисков совершенно по иному моделирует общий размер страховых выплат. Основная идея в том, что требования по страховому портфелю в целом представляют собой случайный процесс. Этот тип моделей можно проиллюстрировать так:
Число требований о выплате по всему страховому портфелю имеет распределение Пуассона со средним l . Размер страховой выплаты подчиняется экспоненциальному распределению со средним q . Размеры страховых выплат независимы друг от друга и от числа предъявляемых требований о выплате. Общий размер страховых выплат представляют собой пример сложного распределения Пуассона.
Математическая модель коллективных рисков строится следующим образом: Пусть
N - число требований о выплате, сделанных в рамках страхового портфеля за данный отрезок времени. Пусть Xi размер i-й выплаты. Тогда![]()
соответствует общей сумме выплат произведенных за данный отрезок времени. Как
N, так и X1,...,Xn являются случайными величинами.Обычно предполагается, что
Среднее, дисперсия и производящая функция моментов общей суммы выплат имеют вид
![]()
![]()
![]() (5.3)
(5.3)
Пример 5.3.
Предположим, что число требований о выплате имеет геометрическое распределение, т.е. функция плотности N имеет вид![]() ,
,
где
0<q<1, p=1-q. Для того, чтобы применить (5.3) необходимо знать MN(t).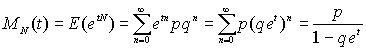
Тогда
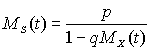
Предположим, что размеры выплат распределены экспоненциально со средним q , тогда
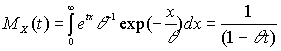
и подставляя полученное выражение в формулу для
MS(t) имеем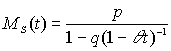 .
.
Пусть G(S)=Pr(S£ s) - функция распределения для S; Если ![]() есть n - кратная свертка распределения Xj, т.е.
есть n - кратная свертка распределения Xj, т.е.
![]()
и
![]() ,
,
то
![]() (5.4)
(5.4)
Замечание.
Если распределение выплат дискретно и возможные значения N малы, то с (5.4) легко работать. Иногда распределение X1+...+Xn может находится в том же классе распределения, что и общее распределение всех Xi; это происходит, например, когда Xi имеют нормальное распределение, или когда общим является гамма-распределение.S ~ CP(l ,F), если
В этом случае
![]() (5.5)
(5.5)
![]() (5.6)
(5.6)
![]()
![]()
Пусть S1,S2,...,Sm взаимно независимые случайные величины, такие что Si~CP(li,Fi) для каждого i. Пусть S=S1+...+Sm. Тогда S~ CP(l ,F), где
![]() , где
, где ![]() . (5.7)
. (5.7)
Пример 5.4.
Страховой портфель содержит 10 000 договоров страхования жизни сроком на год. Половина из них имеет страховую сумму £10 000, а другая £20 000. Вероятность того, что страхователь предъявляет требования о выплате составляет 0,04. Каково распределение общего размера страховых выплат по указанным договорам страхования?Решение.
I. Решим проблему с использованием индивидуальной модели риска. Пусть N1 - число страховых выплат размера £10 000, а N2 - число страховых выплат размера £20 000, тогда N1~В(5000; 0,04), N2~В(5000; 0,04). Общий размер требований о выплате, подсчитываемый по формуле![]()
имеет сложное биномиальное распределение.
Используя (5.1) и (5.2), найдем
![]() (5.8)
(5.8)
![]() (5.9)
(5.9)
Будем считать, что распределение
S близко к![]()
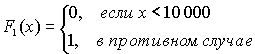
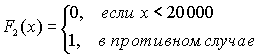
Рассматривая полученные результаты совместно, находим, что общий размер страховых выплат имеет сложное распределение Пуассона с l =400 и
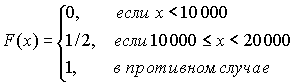
Следствием того, что мы смотрим на распределение общего размера страховых выплат как на сложное распределение Пуассона является то, что общий размер страховых выплат рассматривается теперь как случайная величина, принимающая значения между 10 000 и 20 000 с одинаковой вероятностью. Это противоречит истинной ситуации, когда ровно половина страховых сумм составляют
£10 000, а оставшиеся - £20 000.Вычислим среднее и дисперсию общего размера страховых выплат, предполагая, что он подчиняется сложному распределению Пуассона.
Xi | 10 000 | 20 000 |
pi | 1/2 | 1/2 |
![]()
![]()
Используя (5.5) и (5.6), (5.7), находим
![]() (5.10)
(5.10)
![]() (5.11)
(5.11)
Сравним среднее и дисперсию, полученные двумя способами. Средние, подсчитанные в (5.8) и (5.10) совпадают, поскольку Пуассоновская аппроксимация биномиального распределения дает то же среднее, т.е. l
=np. Дисперсия сложного распределения Пуассона в (5.11) несколько больше, чем дисперсия, полученная в (5.8), ибо дисперсия биномиального распределения равна npq < np = l, т.е. меньше дисперсии соответствующего распределения Пуассона.Если N велико, то в силу центральной предельной теоремы S будет (приближенно) иметь нормальное распределение со средним m=E(S) и дисперсию s2=V(S).
Если
N мало, то эта аппроксимация будет плохой, как для сложного пуассоновского, так и для сложного отрицательного биномиального распределения, асимметрия S всегда положительна, а нормальное распределение (с нулевой асимметрией) особенно плохо аппроксимирует правый хвост.Предположим, что S @ V + k, где k постоянна, а V ~ G(a ,b ). Подбираем a,b ,k путем подгонки первых трех моментов Sк первым трем моментам V + k.
При подсчете вероятностей часто бывает полезным использовать тот факт, что если
V ~ G(a ,b ), тоПусть G(x) - функция распределения для S. Приближенно
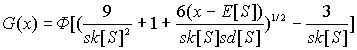 ,
,
если
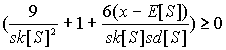 ,
,
где
ks[S] - коэффициент асимметрии S;sd[S] - стандартное отклонение S.
Рекуррентное вычисление
G(x).Пусть
pn=Pr(N=n). Если размеры требований выплат Xj распределены на целых числах без нулевых требований выплат, т.е. если Xj распределено на {1,2,3,...}, при Pr(Xj=k)=fk и если pn таково, что![]()
![]()
Пуассоновское, отрицательное биномиальное и биномиальное распределение имеют свойство
![]() для некоторых a,b.
для некоторых a,b.
Требования выплат распределяется между непосредственным страховщиком (НС) и перестраховщиком (ПС).
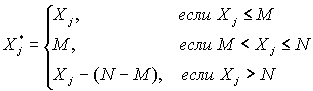
а ПС выплачивает
Xj**, где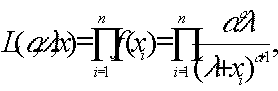
Часто допускается отсутствие верхнего порога, т.е.
N=¥.Для НС можно использовать все результаты, полученные по совокупным распределениям, заменяя распределение
Xj распределением Xj*. В частности, если совокупные требования выплат - сложные пуассоновские, то таковыми являются и совокупные требования выплат перестраховщика (и аналогично для любого сложного распределения S).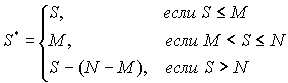
а ПС платит
S**, где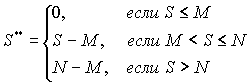
Задачи
№ Пункта | Рекомендуемые задачи |
5.1 | 5.1, 5.2, 5.3, 5.4, 5.5, 5.6, 5.7 |
5.2 | 5.8, 5.9, 5.10, 5.11, 5.12, 5.13, 5.14, 5.15, 5.16, 5.17, 5.18, 5.19 |
5.1.
Пусть Ii, i= 1,2,...,n - независимые случайные величины, такие, что Рr(Ii=1)= pи Рr(Ii = 0) = q = 1— р. Пусть X=а) Каково распределение
X ?b
) Покажите, что Е( Ii ) = р и V(Ii)=pq.с) Получите среднее и дисперсию биномиальной случайной величины.
5.2.
Вероятность предъявления требования о выплате по срочному договору страхования равна 0.05. Если требование о выплате имеет место, его размер подчиняется распределению Парето Р(3, 1000). Используя второй метод предыдущего примера, найдите среднее значение и среднее квадратическое отклонение размера требования о выплате.Подсказка: используйте упражнение
3.2.5.3.
Страховая компания заключает договоры страхования жизни сроком на год. В таблице 5.2 представлена информация об указанном страховом портфеле: число заключенных договоров страхования, возрасты страхователей x, вероятности предъ-явления требований о выплате qx и размеры страховых сумм.Таблица
5.2:Информация о 1000 договорах страхованияВозраст, x | Количество договоров | qx | Страховая сумма |
40 | 4000 | 0,001 | 4 |
50 | 3500 | 0,004 | 5 |
60 | 2500 | 0,010 | 6 |
Замечание:
единица измерения страховых сумм - £5000.а) Предполагая, что страхователи независимы, найдите среднее и дисперсию общего размера требований о выплате за год по всем рассматриваемым договорам страхования.
Прокомментируйте ответы
b) и с).
5.4.
Страховщик предлагает договоры страхования отпускников. Вероятность предъявления требования о выплате по такому договору оценивается в 0,1, а размеры требований о выплате следуют экспоненциальному распределению со средним 100. Страховой взнос составляет £12, страховщик заключил 1000 договоров страхования.Страховщик подумывает об установлении франшизы, с тем, чтобы оплачивать только часть требований о выплате, превышающую
£25.5.5.
(продолжение примера 5.4). Предположим, что компания установила уровень собственного удержания в размере £12000, т.е. компания перестраховала большую часть страховых сумм по договорам с более высокими выплатами. Повторите вычисления из примера 5.4, т.е. найдите:а) новые среднее и дисперсию общего размера требований о выплате;
b
) стоимость перестрахования;с) вероятность того, что страховые выплаты плюс перестраховочный взнос превзойдут
240 единиц.Проделайте указанные вычисления также и для случая, когда уровень удержания устанавливается равным
£10000, т.е. половине страховых сумм по договорам с более высокими выплатами.Теперь у нас есть четыре вероятности того, что общие издержки компании превысят
240 единиц.Отсутствие перестрахования
’’ £12000 z= 1.125
’’ £10000 z = 1.118
Используя квадратичную интерполяцию оцените уровень удержания, который минимизирует вероятность того, что страховые выплаты вместе с расходами на перестрахование превзойдут
240 единиц. Иными словами, какой уровень удержания Вы бы порекомендовали установить?а) Вывести формулы в терминах q, m и s2для среднего и дисперсии X.
б) Теперь предположим, что
q=0.1 и
Пусть
X1 и X2 будут случайными величинами, обозначающими размеры требований выплат в наступающем году по двум из этих рисков.
Показать, что среднее этого распределения есть
![]() .
.
Показать, что дисперсия этого распределения есть
![]() .
.
б) Держатели полисов страховой компании принадлежат к одному из двух классов, А и В. Каждый держатель полиса может предъявить, самое большее, одно требование выплаты в год. Если требование выплаты возникло, то его размер имеет усеченное экспоненциальное распределение. В нижеприведенной таблице по каждому классу дано количество держателей полисов в классе, вероятность того, что страхователь предъявит одно требование выплаты в год и параметры усеченного экспоненциального распределения по размерам индивидуальных требований выплат.
Класс | Количество страхователей в классе | Вероятность требования выплаты | Параметры усеченного экспоненциального распределения |
А | 1.000 | 0,05 | 0,01 200 |
В | 5.000 | 0,10 | 0,02 200 |
Можно предположить, что совокупные ежегодные требования выплат для всего портфеля имеют, приближенно, нормальное распределение.
5.8. Покажите, что производящая функция моментов сложного распределения Пуассона такова:
![]()
Подсказка:
Используйте упражнение 2.6 и (5.16).5.9.
Это упражнение продолжает обсуждение упражнения 5.3, начатое в примере 5.7. Используя метод сложных распределений Пуассона, решите b) и с) из упражнения 5.3.5.10.
Страховщик заключил 1500 договоров (общего) страхования и число требований о выплате по каждому договору следует распределению Пуассона со средним 0.015. Распределение размеров (имевших место) страховых выплат приведено в таблице 5.3.Таблица
5.3: Распределение размеров страховых выплат.Размер выплаты | 200 | 400 | 600 | 800 | 1000 |
Вероятность | 0.1 | 0.2 | 0.3 | 0.3 | 0.1 |
а) Найдите среднее и дисперсию распределения страховых выплат
b
) Предположим, что страховщик хочет быть на 95% уверен, что он будет иметь прибыль от указанного бизнеса.Найдите надбавку безопасности, при которой
это достижимо.с) Предположим, что договор имеет франшизу в
£300. Каково среднее и дисперсия общего размера страховых выплат? Какова надбавка безопасности необходимая (и теперь) для того, чтобы страховщик имел прибыли с вероятностью 95%?Совокупные требования по каждому риску имеют сложное пуассоновское распределение. Параметр Пуассона i-го риска есть li, где
li = 0.1 для i=1,2,...,15;
li = 0.15 для i=16,17,...,20;
Распределение суммы отдельного требования по
i-му риску есть логнормальное распределение с параметрами ? и ?, гдеl= 6.095l= 1.0 для i=1,2,...,10;
l= 6.660l= 0.8 для i=11,12,...,20;
а) Вычислить
E[S] и V[S].б) Какова вероятность того, что отдельное требование из данного портфеля превышает
£ 10 000?в) Используя нормальную аппроксимацию распределения
S, оценить вероятность того, что S > 10 000.г) Доказать, что вероятность того, что
S > 10 000 больше вашей оценки в пункте (в) выше.Для единичного полиса в течение одного года пусть Xi, i=1,2,...,N1 обозначает сумму i-того требования, которая включает ремонт автомобиля страхователя без замены разбитого ветрового стекла (N1 обозначает количество таких требований выплат в год), а Yj, j=1,2,...,N2 обозначает полную сумму j-того требования выплаты, включающую ремонт автомашины страхователя и замену разбитого ветрового стекла (N2 обозначает количество таких требований).
Компания предполагает, что:
Пусть
![]() .
.
Результаты анализа показывают, что
N1 + N2 имеет ожидаемое значение 0.25 и что S имеет среднее £250 и среднеквадратическое отклонение £600. Результаты отдельного анализа показывают, что стоимость замены ветрового стекла имеет среднее £200 и стандартное отклонение £30. Согласно подсчетам компании, для 40% всех требований выплат, связанных с ремонтом автомобиля страхователя также требуется и ремонт разбитого ветрового стекла.а) Рассчитать среднее и стандартное отклонение стоимости ремонта автомобиля страхователя по единичному полису в течении одного года, исключив стоимость ремонта разбитого ветрового стекла.
б) Кратко прокомментировать какое-либо из приведенных выше предположений, кажущееся вам неоправданным.
Другими словами, если
X есть сумма единичного требования выплаты до перестрахования, а Y есть сумма, выплачиваемая перестраховщиком, то![]() ,если
,если ![]() , (1)
, (1)
![]() ,если
,если ![]() , (2)
, (2)
![]() ,если
,если ![]() . (3)
. (3)
и страховщик платит
X-Y.Пусть
VI и VR обозначают дисперсии совокупных требований выплат, оплачиваемых страховщиком и перестраховщиком, соответственно.а) Привести интегральные формулы для
VI и VR в терминах l, f(x), M1и M2.б) Показать, что
VI и VR£V.в) Вычислить
VI , при заданных![]()
Показать, что удерживаемая величина требования выплаты имеет распределение Парето с параметрами a=2.5, l =22 500.
б) Страховщик также покупает полис перестрахования превышения убытков по данному риску у другого перестраховщика В. Положения перестрахования превышения убытков применяются к суммам требований выплат, остающихся после применения договора о квотном разделении. Согласно полису перестрахования превышения убытков, превышение (если таковое имеется) суммы каждого требования выплаты величины
£200 000 оплачивается перестраховщиком В в пределах максимальной выплаты размером £100 000 по каждому требованию выплаты.Перестраховщик не информирует о требованиях выплат по риску, который не вызывает выплат по полису перестрахования превышения убытков.
0 £ a £ b £¥и для любого положительного целого числа m
![]() ,
,
где
f есть функция плотности для Y, Ф есть стандартизованная функция нормального распределения, и![]() ,
,
![]() .
.
б) Годовые совокупные требования выплат по некоторому риску имеют сложное пуассоновское распределение. Параметр Пуассона есть l , суммы единичных требований выплат имеют логнормальное распределение с параметрами m и s . Количество требований выплат в прошлом году и сумма
i-го требования выплаты обозначаются через n и yi, соответственно, где i=1,2,...,n.![]()
где суммируются
n требований выплат, показать, что![]()
![]() ,
,
где
N представляет общее количество требований выплат на будущий год, и![]() ,если
,если ![]() ,
,
![]() ,если
,если ![]() ,
,
![]() ,если
,если ![]() .
.
Используя оценки
5.16. Случайная величина S представляет совокупное требование выплат по некоторому риску на протяжении 1 года. S имеет сложное пуассоновское распределение с параметром Пуассона l =10 и суммами единичных требований выплат Y1,Y2,...,YN(T), распределенных таким образом, что для всех j=1,2,...,N(T), Zj=ln(Yj) имеет гамма-распределение с функцией плотности
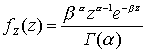 ,
,
где a
=65 ,b =9.0.а) 1) Показать, что общая сумма плотности
Yj есть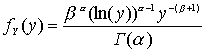 ,
,
значение a
,bсм. выше.б) Использовать нормальное приближение к распределению совокупных требований выплат для оценки вероятности того, что
S > 40 000.в) Использовать переведенное гамма-приближение к распределению совокупных требований выплат для оценки вероятности того, что
S > 40 000.г) Кратко прокомментировать различия в оценках в пунктах (б) и (в).
![]() ,если
,если ![]() ,
,
![]() ,если
,если ![]() .
.
Предположим, что
N имеет биномиальное распределение с параметрами n и p, и что Yi распределено на положительных целых числах. Пусть fk и gj определены следующим образом:![]() , k=1,2,3,...
, k=1,2,3,...
![]() , j=0,1,2,...
, j=0,1,2,...
а) Показать, что
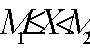 ,
,
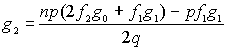
и сформулировать, но не доказывать общую формулу для
gj в терминах n, p, j, fi и gj-k, где k=1,2,...,j.б
) При n = 10, p = 0.1, E[Yi] = 5.5 и V[Yi] = 7.25 вычислить среднее значение и дисперсию X.в) Предполагая дополнительно к данным в вышеприведенном пункте (б), что
f1=0.1, вычислите среднее значение и дисперсию Z, где![]() , если
, если ![]() ,
,
![]() , если
, если ![]() .
.
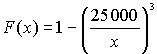 для 25 000 £x < ¥
для 25 000 £x < ¥
Имеется 10 000 застрахованных наемных работников.
а
) Вычислить среднее значение и дисперсию полных ежегодных расходов по требованиям выплат для этого полиса.б
) Используя принцип дисперсии и нормальную аппроксимацию для распределения совокупных требований выплат, показать, что коэффициент премиальной нагрузки, который гарантирует, что страховой взнос превышает требования выплат с вероятностью 0.8, равен 5.0 х 10-6. Каков коэффициент нагрузки для этого же уровня обеспечения, если использовать принцип ожидаемой стоимости?в
) После изменения правил схемы страховое возмещение, выплачиваемое в связи со смертью застрахованного, ограничено максимальной суммой £100 000. Используя премиальную нагрузку из (б), найти пересмотренную премию по принципу дисперсии. Используя эту премию и нормальную аппроксимацию распределения совокупных требований выплат, найти вероятность того, что требования выплат превысят страховые взносы в течении полисного года.г) Повторить пункт (в), используя принцип ожидаемой стоимости и нагрузку для принципа ожидаемой стоимости из (б).
д
) Кратко обсудить различия, возникающие между принципом дисперсии и принципом ожидаемой стоимости для премий, после изменения страхового возмещения.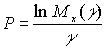
выводится из страхового взноса, рассчитанного по принципу нулевой полезности.
б
) Требования выплат по риску имеют сложное пуассоновское распределение с параметром Пуассона q= 20. Размеры индивидуальных требований выплат, исчисленные в тысячах фунтов £1 000 имеют моменты возле нуля:Страховщик рассчитал страховые взносы, используя экспоненциальный принцип.