Глава 4.
Теория достоверности.Теория доверительных оценок дает метод для исчисления страховых доверительных взносов по краткосрочным договорам страхования при использовании
Двумя существенными чертами доверительного взноса является то, что он представляет собой линейную функцию от полученных ранее прямых данных о риске и то, что он может регулярно пересматриваться по мере поступления новых данных.
Доверительный взнос (премия правдоподобия) для индивидуального риска имеет вид
PCR = Z PR + (1 - Z) PC , 0 < Z £ 1,
(4.1)где
PR - оцененная премия, основанная на опыте самого индивидуального риска,PC - оцененная премия, основанная на опыте других подобных рисков. PCR - взвешенное среднее значение этих двух оценок. Z - коэффициент доверия (правдоподобия, достоверности) - это мера того, насколько надежными считает страховая компания прямые данные о новом риске. Часто доверительный взнос (4.1) выражают формулой:доверительный взнос =
Возникает интересный практический вопрос: сколько данных необходимо иметь по оцениваемой страховке, чтобы можно было принять коэффициент доверия равным единице? Для определения достаточности числа данных по оцениваемой страховке, чтобы можно было принять Z=1, актуарии Северной Америки используют следующий критерий: относительная погрешность между действительным нетто-взносом (b ) и оценкой, полученной на основе имеющихся данных (![]() ), не должна превышать заданной величины (kb) с заданной вероятностью p. Данные “полностью (k,p) - достоверны”, если
), не должна превышать заданной величины (kb) с заданной вероятностью p. Данные “полностью (k,p) - достоверны”, если
![]() (4.2)
(4.2)
Пример 4.1.
Предположим, что ежегодное число страховых случаев подчиняется распределению Пуассона с неизвестным параметром l . Пусть имеются предыдущие данные по этой страховке за
n лет, причем полное число наблюдаемых страховых случаев равно M. Оценить частоту страховых случаев.Решение.
Оценка l , основанная на этих данных, есть
M ~ P (l n )
и, используя нормальное приближение, получаем:
M ~ N (l n , l n )
(4.3)Из формулы (4.2) получаем, что данные полностью
(k,p) - достоверны, если![]()
или
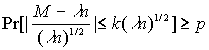 (4.4)
(4.4)
Чтобы закрепить понимание идеи, примем
k = 0.05 и p = 0.9, т.е. потребуем, чтобы вероятность того, что оценка l лежала в пределах 5% от действительного значения, составила 90%. Используя формулу (4.3) и таблицы стандартного распределения, можно показать, что для выполнения (4.4) необходимо![]()
![]() (4,5)
(4,5)
Данные по самой страховке были бы полностью (0,05;0,9) - достоверными, если число предшествующих страховых случаев было бы не меньше 1082, для практических целей (4.5) можно заменить на
M
³ 1082Таким образом, риск является вполне (
k,p) достоверным, 0<k<1, 0<p<1, если имеется достаточно данных о том, что частота предъявленных требований выплат, находится в пределах 100k% основного ожидаемого значения, больше p, т.е.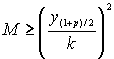 ,
,
где
M- количество требований выплат имевших место за период nлет;l- истинное значение ожидаемого количества требований выплат
ye = Ф-1 (e )
Обычно используемым стандартом является
k = 0.05 и p = 0.95.Если предыдущие данные по страховке недостаточны, чтобы их можно было считать полностью достоверными, то необходимо использовать дополнительные данные, а также определить коэффициент Z.
Если размеры индивидуальных требований выплат
Yj имеют моменты E(Yj)=p1, E(Yj2)=p2, то критерием полного правдоподобия служит: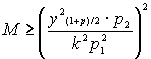 (4.6)
(4.6)
Если риск не является вполне правдоподобным, используется коэффициент правдоподобия для стандарта
(k,p)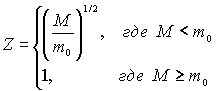 (4.7)
(4.7)
где
m0 есть количество требований выплат, необходимых для полного правдоподобия. Вывод формул (4.6) и (4.7) приведен в приложении 4.Основной сложностью подхода к теории достоверности является отсутствие удовлетворительного метода определения коэффициента Z (см. Приложение 4), когда данные по оцениваемой страховке нельзя считать полностью достоверными. Байесовский подход преодолевает эту сложность и имеет ряд других преимуществ.
Апостериорная байесовская оценка частоты требований выплат или их размера (относительно квадратичных убытков) удовлетворяет условиям правдоподобия оценки. Апостериорная байесовская оценка постоянного, но неизвестного параметра q , связанного с каким-либо риском, имеет вид
![]() ,
,
где
Предполагается, что частота требований индивидуального риска имеет P(l ) распределение с неизвестным l , моделируемым с использованием априорного распределения G(a ,l ), и тогда
![]() , где
, где ![]() .
.
Вывод формул представлен в приложении 5.
Пример 4.2.
Страховщику необходимо назначить взнос по схеме группового страхования жизни. Информация, данная страховщику, такова:
![]() для всех i,
для всех i,
где
![]() - сила смертности в возрасте i, согласно таблице дожития А 1967-70 Ultimate,
- сила смертности в возрасте i, согласно таблице дожития А 1967-70 Ultimate,
![]() - параметр, значение которого одинаково для всех i, но неизвестно.
- параметр, значение которого одинаково для всех i, но неизвестно.
Неопределенность в отношении значения q моделируется тем, что qсчитается случайной величиной: q~ N(4;4), поэтому априорное среднее q равно 1, а его априорная дисперсия 1/4.
Страховщик предполагает, что число выплат в прошлом году имеет пуассоновское распределение с параметром
![]() , (4.8)
, (4.8)
что составляет нетто-взнос, который следовало бы назначить, если было бы известно значение q . Поскольку q неизвестно, его следует оценить, используя данные по предыдущим выплатам.
а) Если у страховщика нет данных по предыдущим выплатам, относящимся к этой схеме, наилучшей оценкой q является
E[q ]=1. В этой случае нетто-взнос равен![]() (4.9)
(4.9)
б) Предположим, что страхование по схеме осуществлялось в течение
m лет. Обозначим через xj число смертей, случившихся j лет назад. Обозначим через tj коэффициент![]() ,
,
где
nij - число страхуемых возраста i в схеме jлет тому назад. Следовательно, tjпредставляет собой математическое ожидание числа смертей в соответствии с А 1967-70 Ultimate, а xj - реализация случайной переменной Xj, гдеXj~ P ( q tj )
Тогда, апостериорное распределение q при заданных
x1,x2,...,xm есть![]() , (4.10)
, (4.10)
а наилучшая оценка нетто-взноса есть:
![]()
Формулу можно переписать как:
![]() , (4.11)
, (4.11)
где
![]()
Чтобы проиллюстрировать численно эти формулы, предположим, что
m=5, x1=1, t1=2.5.Тогда оценка q на основе данных, в соответствии с выражением (4.10) равна 0.77, и, следовательно, достоверный взнос, задаваемый выражением (4.11), на 23% ниже, чем нетто-взнос, задаваемый выражением (4.9).
Предположим теперь, что
![]()
Тогда (4.10) дает оценку q , равную 1.36, и достоверный взнос на 36% выше, чем (4.9).
Предполагается, что размеры требований нормально распределены при постоянном, но неизвестном среднем q и известном стандартном отклонении s1. Априорное распределение также нормально со средним m и стандартным отклонениемs2. Тогда
![]() ,где
,где 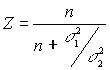 .
.
Вывод формул представлен в приложении 6.
Пример 4.3.
Дано:
X1|q~ N(8.6;4); X2|q~ N(9.4;4); X3q~ N(11.2;4);q~ N(10,1). Вычислить доверительный взнос.Решение.
Косвенные данные:
Прямые данные:
Тогда
Z=3/7; доверительный взнос = 3/7 * 9,5 + 4/7 * 10 = 9,79.Байесовский подход срабатывает лишь в небольшом числе случаев и требует наложения сильных предположений на распределение (знание априорного распределения). Наиболее эффективным является использование эмпирического подхода для нахождения оценки правдоподобия, которая близка к апостериорной байесовской статистике.
Эмпирическая байесовская техника также позволяет использовать данные от группы рисков для оценки параметров “априорного” распределения.
Предположения.
Пусть Xj, j=1,2,...,n обозначают совокупные требования выплат по некоторому риску. Предполагается, что они одинаково распределены, причем это распределение зависит от некоторого фиксированного, но неизвестного параметра q , такого что средним значением Xj для всех j является некоторая функция от q , обозначаемая через m(q ). Целью является нахождение оценки E(m(q )|x), которая имеет вид оценки правдоподобия, где x=(x1,x2,...,xn) есть совокупность наблюдаемых значений Xj. Предположение относительно Xj и q следующие:
Оценка совокупных требований выплат по риску.
Эмпирический байесовский доверительный взнос дается формулой
![]() ,
,
где
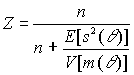
Вывод формул приведен в приложении 7.
Оценивание параметров.
Необходимо получить оценки E[m(q )], V[m(q )], E[s2(q )].Допустим, что есть группа из N рисков с данными за n лет по совокупным требованиям выплат для каждого риска. Допустим, что требования выплат в разные годы по каждому риску одинаково распределены и зависят от постоянного, но неизвестного параметра qi для i-го риска, i=1,2,...,N. Пусть Xij обозначает требования выплат по риску i в год j, i=1,2,...,N, j=1,2,...,n.
Тогда:
С учетом данных по этим рискам
(x1,1,...,xN,n) несмещенными статистиками для этих параметров служат: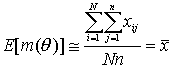
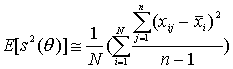
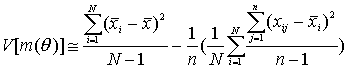
где
Пример 4.4.
Имеется сверхсовокупность с q ~
N(10,1), три риска с q =8,6; 9,4; 11,2. Данные по трем рискам приведены в таблице 4.1.Таблица 4.1.
Год 1 | Год 2 | Год 3 | Среднее | Дисперсия | |
Риск 1 | 9,9 | 8,3 | 10,3 | 9,5 | 1,12 |
Риск 2 | 10,9 | 11,6 | 7,5 | 10,0 | 4,81 |
Риск 3 | 11,0 | 9,7 | 10,5 | 10,4 | 0,43 |
Найти доверительный взнос.
Решение.
![]()
![]()
![]()
![]()
Достоверный взнос для первого риска равен:
![]()
Пример 4.5.
В таблице 4.2 приведены данные по страхованию промышленных объектов от пожаров за шесть лет подряд для пяти страховых компаний. Величины выплат пересчитаны так, чтобы устранить влияние инфляции, и измерены в некоторых условных единицах.
Таблица 4.2.
Номер | Годы | |||||
страховщика | 1 | 2 | 3 | 4 | 5 | 6 |
1 | 103 | 73 | 32 | 102 | 78 | 87 |
2 | 112 | 138 | 29 | 93 | 104 | 71 |
3 | 135 | 155 | 121 | 123 | 77 | 139 |
4 | 91 | 106 | 109 | 111 | 116 | 81 |
5 | 67 | 133 | 65 | 93 | 118 | 89 |
Используем эмпирическую байесовскую модель для расчета эмпирической байесовской достоверной оценки нетто-взноса для первого страховщика. Предположим, что для данного страховщика выплаты идентично распределены от года к году. Поскольку влияние инфляции устранены, резонно предположить, что число страховых полисов и условия страхования меняются из года в год незначительно. Оценим
E[m(q )], V[m(q )], E[S2(q )].Найдем среднее и дисперсию для каждого страховщика и занесем в таблицу 4.3.
Таблица 4.3.
Номер страховщика i |
|
|
1 | 79,17 | 683 |
2 | 91,17 | 1413 |
3 | 125,00 | 704 |
4 | 102,33 | 181 |
5 | 94,17 | 739 |
![]()
![]()
![]()
Оценка коэффициента достоверности
![]()
Достоверный взнос для первого страховщика равен
![]()
В предыдущей модели рассматривалась согласованность рисков в отношении размера страхового покрытия по каждому риску в каждый год. В данной модели полученный результат обобщается на риски с ежегодно изменяющимся объемом, и обобщается процедура оценивания, что позволяет использовать данные по рискам, которые аналогичны оцениваемым, но которые могут отличатся по объему риска.
Предположения.
Пусть Yj, j=1,2,...,n обозначают совокупные требования выплат по некоторому риску и пусть Pj обозначает объем риска в год j. Объем риска предполагается известным и не является случайной величиной.
Тогда Xj=Yj/Pj, j=1,2,...,n есть объем совокупного требования выплат в j-й год на единицу объема риска.
Предположим, что Xj имеет распределение, зависящее от некоторого фиксированного, но неизвестного параметра q такого, что среднее значение Xj для всех j является некоторой функцией от q , обозначаемой m(q ). Целью является нахождение оценки E[m(q )|x], которая имеет форму оценки правдоподобия, где x=(x1,x2,...,xn) есть множество наблюдаемых значений Xj. Предположения относительно Xj и q следующие
Оценка правдоподобия совокупных требований выплат
на единицу объема риска.
![]() ,
,
где
![]()
и
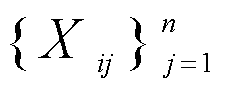
Вывод формул представлен в приложении 8.
Оценивание параметров.
Найдем оценки для E[m(q )], V[m(q )], E[s2(q )]. Предположим, что имеется группа из N рисков с данными за n лет по совокупным требованиям выплат для каждого риска. Пусть Yij будут (случайными) совокупными требованиями выплат по риску i в год j при соответствующем объеме риска Pij. Тогда Xij=Yij/Pijи предположим, что
Пусть
x1,1,...,xN,n наблюдаемые значения X1,1,...,XN,n.![]()
![]() ,
,
![]()
тогда несмещенными оценками будут:
![]()
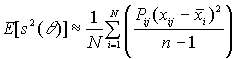
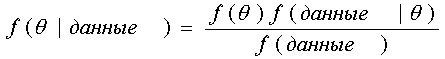
Пример 4.6.
Страховая компания заключила договоры по страхованию автомобилей с семью компаниями, сдающими автомобили напрокат и имеющими парки аналогичных машин. Каждая прокатная компания имеет один договор, охватывающий все автомобили на один и тот же период. Ниже приведены данные для каждой из семи компаний, включающие совокупные выплаты Y за пять лет подряд в сотнях фунтов стерлингов и число застрахованных автомобилей P в эти годы.Номер | Годы | ||||
компании | 1 | 2 | 3 | 4 | 5 |
Y:P | Y:P | Y:P | Y:P | Y:P | |
1 | 100:80 | 57:80 | 20:83 | 180:85 | 38:85 |
2 | 2:5 | 2:5 | 0:5 | 7:5 | 1:5 |
3 | 4:20 | 12:20 | 15:20 | 0:23 | 2:26 |
4 | 5:10 | 0:10 | 1:9 | 1:9 | 4:10 |
5 | 0:15 | 3:20 | 3:25 | 0:25 | 2:30 |
6 | 6:10 | 0:11 | 0:11 | 0:11 | 12:12 |
7 | 14:30 | 4:29 | 43:29 | 7:30 | 10:30 |
Чтобы рассчитать достоверные взносы для всех компаний, при условии, что они в наступающем году будут иметь 87, 5, 30, 10, 35, 13 и 30 автомобилей соответственно, в рамках эмпирической байесовской теории достоверности воспользуемся моделью Бюльмана-Штрауба, рассматривается число автомобилей в каждом случае как объем страхования. Данная модель будет приемлема, если предположить, что для данной компании величина выплат на каждый автомобиль в течении года имеет постоянное среднее и дисперсию в течении пяти дет, когда собирались данные, и, конечно, среднее и дисперсия останутся неизменными в наступающем году.
Расчеты таковы
Номер компании |
|
|
1 | 4,3 | 0,9654 |
2 | 25 | 0,4800 |
3 | 109 | 0,3028 |
4 | 48 | 0,2292 |
5 | 115 | 0,0696 |
6 | 55 | 0,3273 |
7 | 148 | 0,5270 |
Отметим, что
Yij=XijPij, так что![]()
![]()
Теперь полезно записать полученные значения
Xij для каждой компанииНомер | Год | ||||
компании | 1 | 2 | 3 | 4 | 5 |
1 | 1,2500 | 0,7125 | 0,2410 | 2,1176 | 0,4471 |
2 | 0,4000 | 0,4000 | 0,0000 | 1,4000 | 0,2000 |
3 | 0,2000 | 0,6000 | 0,7500 | 0,0000 | 0,0769 |
4 | 0,5000 | 0,0000 | 0,1111 | 0,1111 | 0,4000 |
5 | 0,0000 | 0,1500 | 0,1200 | 0,0000 | 0,0667 |
6 | 0,6000 | 0,0000 | 0,0000 | 0,0000 | 1,0000 |
7 | 0,4667 | 0,1379 | 1,4828 | 0,2333 | 0,3333 |
Для каждой компании рассчитаем две статистики
Номер компании |
|
|
1 | 190,79 | 240,96 |
2 | 5,84 | 1,25 |
3 | 9,41 | 19,56 |
4 | 1,80 | 8,69 |
5 | 0,39 | 33,71 |
6 | 9,71 | 14,04 |
7 | 34,71 | 35,67 |
![]()
![]()
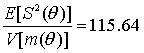
Для компании 1 получаем достоверный взнос на единицу объема
![]()
а оценка нетто-взноса на предстоящий год равна
![]() , т.е. 7660
, т.е. 7660
Для компании 2 оценка нетто-взноса равна
![]() , т.е. 290
, т.е. 290
Отметим, что в отличии от эмпирической байесовской модели, коэффициент достоверности
Z в модели Бюльмана-Штрауба различен для каждой страховки, так как он зависит от суммы объемов страхования для данной оцениваемой страховки.Оценки нетто-взносов для других компаний равны:
Компания 3: 1380
Компания 4: 500
Компания 5: 1190
Компания 6: 670
Компания 7: 1690
Задачи
№ Пункта | Рекомендуемые задачи |
4.2.1 | 4.1 |
4.2.2. | 4.2 |
4.3.1. | 4.3, 4.4 |
Общие задачи | 4.5, 4.6, 4.7, 4.8, 4.9, 4.10, 4.11, 4.12 |
4.1.
Покажите, что математическое ожидание апостериорного распределения l после n лет имеет видпокажите также, что последние выражение можно переписать так:
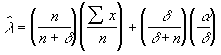
Что говорит это выражение об относительной значимости априорной информации
? Информации по договору страхования, накапливающейся с течением времени?4.2.
Предположим, что сверх-совокупность рисков, такова, что q~N(100,100), а распределение отдельных рисков условные по q , таковы, что xi/q~ N(q ,10)а) Сделайте набросок графика плотности распределения сверх-совокупности рисков.
б) Выберите 5 возможных реализаций q (псевдослучайным способом) из сверх-совокупности и набросайте график соответствующих плотностей.
в) Покажите, что коэффициент доверия
Z равенг) Рассмотрите первый из выбранных рисков. Выберите 4 значения для общих размеров требований о выплате в 4 последовательных сроках страхования. Вычислите доверительный взнос после 0,1,2,3 и 4-го срока и сравните ответы с m и
4.3.
Данные приведенные ниже, показывают общие размеры страховых выплат по страхованию от огня промышленных объектов, полученные за шесть (последовательных) лет работы пятью страховыми компаниями. Для того, чтобы устранить влияние инфляции выплаты измеряются в сопоставимых единицах.Таблица
4.4: Общие размеры страховых выплат пяти страховых компаний.
1 |
2 | Год 3 |
4 |
5 |
6 | |
Риск 1 | 103 | 73 | 32 | 102 | 78 | 87 |
Риск 2 | 112 | 138 | 29 | 93 | 104 | 71 |
Риск 3 | 135 | 155 | 121 | 123 | 77 | 139 |
Риск 4 | 91 | 106 | 109 | 111 | 116 | 81 |
Риск 5 | 67 | 133 | 65 | 93 | 118 | 89 |
Требуется определить эмпирический байесовский доверительный взнос на предстоящий год с использованием модели, построенной в предыдущем пункте. Заметьте, что использование этой модели предполагает, что годичные страховые выплаты одинаково распределены. Поскольку мы игнорируем инфляцию это представляется разумным, ибо обычно в течение ряда лет число заключаемых договоров и правила страхователя не претерпевают значительных изменений.
а) Начните с графического решения. Набросайте график выплат по каждому риску и, ничего не вычисляя, прикиньте грубые оценки для пяти значений
b)
Затем перейдите к точным вычислениям. (Приветствуется работа в команде!) Вы должны получить, что E[m(q )]=98.37; E[s2(q )]=744; V[m(q )]=291. Используйте эти значения для вычисления Z и вычислите доверительный взнос для первой страховой компании.4.4.
Вы вновь можете предполагать, что можно применять эмпирическую байесовскую модель. В этом примере страховщики располагают различным опытом наблюдения за рисками.Таблица
4.5: Общие размеры страховых выплат четырех страховых компанийГод | ||||||
1 | 2 | 3 | 4 | 5 | 6 | |
Риск 1 | 89 | 82 | 102 | 75 | - | - |
Риск 2 | 71 | 85 | 86 | 84 | 67 | 87 |
Риск 3 | 70 | 84 | 82 | 76 | 74 | 64 |
Риск 4 | 88 | 87 | 79 | 70 | - | - |
а) Используйте графический метод, описанный а предыдущем упражнении, для быстрого получения грубой оценки
Z, скажем, для первого риска.b
) Вычислите для четырех рисков средние и дисперсии. Вы столкнетесь с тем, что у компаний различный опыт наблюдения за рисками. Один из путей решения этой проблемы - игнорировать ее и повторить решение, как в п. b) предыдущего упражнения. Сделайте это. E[m(q )]= 80.75; E[s2(q )]= 83.37; V[m(q )]= 24.25. Получите коэффициент доверия Z и вычислите доверительный взнос по риску 1.с) Лучшее решение
- это попытаться принять во внимание различный объем информации у страховщиков. Используйте взвешенные средние для получения более качественных оценок E[m(q )] иE[s2(q )]. Улучшить оценку V[m(q )] довольно трудно и поэтому используйте величину, найденную в b). Вычислите коэффициентдоверия и доверительныйвзнос по первому риску.d)
Сравните ответы, полученные в а), b), с).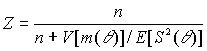 ,
,
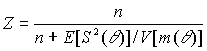 .
.
б) Подтвердите свой ответ на вопрос пункта (а), прокомментировав, как
Z должно вести себя в качестве функции от n, отГод | 1 | 2 | 3 | 4 | 5 | 6 |
(Y;P) | (Y;P) | (Y;P) | (Y;P) | (Y;P) | (Y;P) | |
Номер риска | ||||||
1 | (243;80) | (304;85) | (195;85) | (270;90) | (250;90) | (292;95) |
2 | (80;25) | (78;20) | (65;20) | (42;20) | (75;25) | (63;20) |
Оценка премии правдоподобия на единицу объема риска в будущем году по риску номер 1 есть 2.72, а получаемый коэффициент правдоподобия по этому риску равен 0.75.
а) Вычислить премию правдоподобия на единицу объема риска в следующем году по риску номер 2 и соответствующий коэффициент правдоподобия.
б) Кратко пояснить, почему получаемые коэффициенты правдоподобия по этим двум рискам не одинаковы.
Таблица 1
Количество требований выплат
YГод j | ||||||||
Риск i | 1 | 2 | 3 | 4 | 5 |
|
| |
1 | 122 | 144 | 99 | 95 | 135 | 199,0 | 1866,0 | |
2 | 72 | 78 | 98 | 88 | 90 | 85,2 | 423,0 | |
3 | 87 | 71 | 91 | 88 | 70 | 81,4 | 405,2 | |
4 | 67 | 105 | 94 | 71 | 68 | 81,0 | 1210,0 | |
Использовать эти данные для подсчета оценки частоты требований выплат для компании 1 по эмпирической байесовской теории правдоподобия (ЭБТП), модель1.
б) Обосновать, почему ЭБПТ, модель 2 была бы более пригодна для этих данных, чем модель 1. Предложить меры объема риска, которые могли бы быть использованы.
в) Единственной доступной мерой объема риска служит количество полисов, выписанных каждой страховой компанией. Они приведены в таблице 2 ниже. В таблице 3 дана краткая статистика с использованием обычных обозначений, в частности,
Таблица 2
Количество полисов
Pij.Риск i | Год j | P | ||||
1 | 2 | 3 | 4 | 5 | ||
1 | 1020 | 1200 | 1055 | 910 | 1310 | 5495 |
2 | 665 | 795 | 1042 | 773 | 951 | 4226 |
3 | 748 | 593 | 844 | 898 | 654 | 3737 |
4 | 765 | 888 | 850 | 874 | 842 | 4219 |
Таблица 3
Риск i |
|
|
1 | 0,5655 | 0,6810 |
2 | 0,2585 | 0,2947 |
3 | 0,2203 | 0,3211 |
4 | 1,0587 | 1,3096 |
Используя данные трех таблиц, вычислить оценку количества требований выплат по ЭБТП, модель 2 в наступающем году для компании 1, считая, что предполагаемый объем риска составляет 1000 полисов.
а) Найти статистику максимального правдоподобия l в терминах
N и n.б) Используя гамма
(a ,b )-априорное распределение для l , найти байесовскую статистику l , по отношению к квадратическим убыткам в терминах N, n, aи b.в) Показать, что байесовская статистика, найденная в пункте (а), есть статистика правдоподобия l
.г) Через 5 лет по риску возникло 19 требований выплат. Через последующие 5 лет по данному риску возникло всего 38 требований выплат. Учитывая, что a
=9 и b=3, найти статистики правдоподобия для l на конец 5-го года и на конец 10-го года.д) Оценка правдоподобия l с использованием модели 1 эмпирической байесовской теории правдоподобия составляет
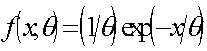
Описать, как
Показать, что
![]() ,
,
где
k>0 есть некоторая постоянная величина, которую вы должны задать, а X представляет собой совокупные требования выплат по данному риску в n-й год.б) Кратко прокомментировать это выражение для
Pn+1.4.10. Множество случайных величин ![]() представляет совокупные требования выплат за n последовательных лет от рисков N. Предполагается, что эти данные удовлетворяют допущениям по модели 1 эмпирической байесовской теории правдоподобия (ЭБТП), т.е. рассматривая вначале i-й риск, требования выплат предполагаются зависящими от неизвестного параметра рискаqi, и
представляет совокупные требования выплат за n последовательных лет от рисков N. Предполагается, что эти данные удовлетворяют допущениям по модели 1 эмпирической байесовской теории правдоподобия (ЭБТП), т.е. рассматривая вначале i-й риск, требования выплат предполагаются зависящими от неизвестного параметра рискаqi, и
![]() - одинаково распределены
- одинаково распределены
![]() - независимы и одинаково распределены
- независимы и одинаково распределены
и для каждой пары различных рисков, Xij и Xkm, i¹ k с ассоциированными параметрами риска qi и qk, (Xij, qi) и (Xkm, qk) независимы и одинаково распределены.
а) 1) Показать, что статистики для ![]() и
и ![]() по модели 1 ЭБТП, данные на страницах с формулами в книге “Формулы и таблицы для актуарных экзаменов”, являются несмещенными. Можно использовать без доказательства тот результат, что для одинаково распределенных случайных величин Y1,Y2,...,Yn с общей дисперсией s2
по модели 1 ЭБТП, данные на страницах с формулами в книге “Формулы и таблицы для актуарных экзаменов”, являются несмещенными. Можно использовать без доказательства тот результат, что для одинаково распределенных случайных величин Y1,Y2,...,Yn с общей дисперсией s2

б) 1) В ниже приведенной таблице даны значения
Xij для каждого из 6 рисков из некоторого множества на протяжении 5 лет. Использовать эти данные для расчета премий правдоподобия модели 1 ЭБТП для риска номер 6.Год, j | |||||||
Риск i | 1 | 2 | 3 | 4 | 5 |
|
|
1 | 75 | 63 | 81 | 78 | 65 | 72,4 | 255,2 |
2 | 72 | 106 | 112 | 77 | 60 | 85,4 | 2072,2 |
3 | 132 | 154 | 148 | 87 | 95 | 123,2 | 3746,8 |
4 | 79 | 88 | 97 | 86 | 85 | 87,0 | 170,0 |
5 | 99 | 75 | 104 | 93 | 91 | 92,4 | 483,2 |
6 | 180 | 141 | 175 | 153 | 81 | 146,0 | 6296,0 |
![]() ,
,
![]() ,
,
![]() при
при ![]() .
.
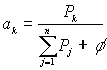 ,
,
где
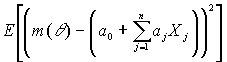 ,
,
есть
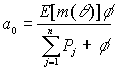
и вывести отсюда коэффициент правдоподобия для модели 2 эмпирической байесовской теории правдоподобия.
б) Страховщик использует модель 2 эмпирической байесовской теории правдоподобия для оценки требований выплат от портфеля полисов, покрывающих убытки от краж по нескольким мелким и средним сериям магазинов.
Ниже приводится резюмирующая статистика по пятилетнему опыту данного множества магазинов, используемая для оценки параметров модели.
P есть число магазинов, покрываемых i-м риском в год j, а Y есть общие потери от краж (в тыс. £) по i-тому риску в год j (используя обозначения из книги “Формулы и таблицы для актуарных экзаменов”):Риск i |
|
|
|
|
1 | 152 | 0,4066 | 1,0669 | 1,3448 |
2 | 14 | 0,2643 | 0,6442 | 0,7829 |
3 | 58 | 0,2759 | 0,2055 | 0,6543 |
4 | 23 | 0,4202 | 0,0381 | 0,1112 |
5 | 45 | 0,5900 | 0,9701 | 3,2722 |
6 | 42 | 0,1714 | 0,2381 | 1,7928 |
7 | 18 | 0,1750 | 0,0238 | 0,6656 |
Всего | 352 | 3,1867 | 8,6238 |
![]() для j=1,2,3,...,n.
для j=1,2,3,...,n.
Эти последовательности удовлетворяют предположениям модели 2 эмпирической байесовской теории правдоподобия.
Показать, что