Глава 2. Распределение потерь.
Для правильного управления страховой компанией фундаментальное значение имеет информация об общем размере требований о выплате за определенный период времени. В этой главе сконцентрировано внимание на одной из составляющих общего размера требований о выплате - на размерах отдельных требований о выплате. Предполагается, что указанные размеры отдельных требований описываются специальными распределениями, называемыми распределениями потерь (убытков).
Обычно предполагается, что распределение требований о выплате находится в некотором классе распределений. Тогда возникает задача оценки параметров, от которых зависят распределения, лежащие в упомянутом семействе. Эти оценки проводятся с помощью данных о требованиях страховых выплат и подходящих методов (например, метода моментов или метода максимального правдоподобия). При решении описанных задач могут возникнуть проблемы: например, из-за того, что размер требований о выплате ограничивается (перестрахование) или, потому, что нужно отсекать требования небольшого размера (франшиза).
Познакомимся с некоторыми техническими приемами, использующимися для описания распределений случайных величин на конкретном примере, который будет использоваться на протяжении всей главы.
Пример 2.1.
В таблице 2.1. приведены данные о размерах 96 отдельных требований о выплате, сделанных по некоторому виду страхования, размеры требований упорядочены для удобства работы с ними.
Таблица 2.1. Размеры (отдельных) требований о выплате (в фунтах стерлингах)
24 | 26 | 73 | 84 | 102 | 115 |
132 | 159 | 207 | 240 | 241 | 254 |
268 | 272 | 282 | 300 | 302 | 329 |
346 | 359 | 367 | 375 | 378 | 384 |
452 | 475 | 495 | 503 | 531 | 543 |
563 | 594 | 609 | 671 | 687 | 691 |
716 | 757 | 821 | 829 | 885 | 893 |
966 | 1053 | 1081 | 1083 | 1150 | 1205 |
1262 | 1270 | 1351 | 1385 | 1498 | 1546 |
1565 | 1635 | 1671 | 1706 | 1820 | 1829 |
1855 | 1873 | 1914 | 2030 | 2066 | 2240 |
2413 | 2421 | 2521 | 2586 | 2727 | 2797 |
2850 | 2989 | 3110 | 3166 | 3383 | 3443 |
3512 | 3515 | 3531 | 4068 | 4527 | 5006 |
5065 | 5481 | 6046 | 7003 | 7245 | 7477 |
8738 | 9197 | 16370 | 17605 | 25318 | 58524 |
Вычислим некоторые статистические характеристики этой таблицы
![]()
![]()
Частично при сглаженные данные показаны на гистограмме, очень большие требования опущены на гистограмме.
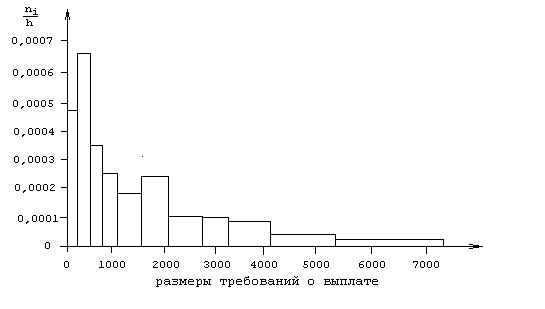
Рис 2.1. Гистограмма размеров требований о выплате (по данным таблицы 2.1).
Из гистограммы видно, что распределение, которое бы хорошо подгонялось под данные, должно быть асимметричным и “длиннохвостым”, одним из таких распределений является экспоненциальное распределение.
Выбрав класс экспоненциальных распределений, необходимо решить две проблемы:
Для оценки параметра экспоненциального распределения используется метод максимального правдоподобия.
Предположим, что x1,...,xn - независимые константы наблюдения, т.е. значения, которые принимала случайная величина X (размер отдельных требований о выплате), следующая экспоненциальному распределению с плотностью
![]()
Оценка максимально правдоподобия (см. п. 1.5.1), это
Таким образом, для описания данных таблицы 2.1. можно рассмотреть экспоненциальное распределение со средним
Произведем тестирование подгонки, используя критерий
Сгруппируем 96 констант наблюдения в 12 классов и установим ожидаемое число элементов в каждом классе равным 96/12=8. Если
F(x) - это функция распределения X ~ E(1/q ), то![]()
Пусть
cj - верхняя граница для элементов, лежащих в j-м классе. Выберем cjиз условия![]()
![]()
Величины
cj приведены в таблице 2.2. - они указывают на границы классов, и в каждом классе указана зарегистрированная (по данным таблицы 2.1) константа и ожидаемая (по построенной модели) величина.Таблица 2.2. Зарегистрированные и ожидаемые величины
(экспоненциальная модель)
Класс | Зарегистрированные частоты, Oi | Ожидаемые частоты, Ei |
0-260 | 12 | 8 |
260-545 | 18 | 8 |
545-860 | 10 | 8 |
860-1212 | 8 | 8 |
1212-1612 | 7 | 8 |
1612-2073 | 10 | 8 |
2073-2618 | 5 | 8 |
2618-3285 | 6 | 8 |
3285-4145 | 6 | 8 |
4145-5357 | 3 | 8 |
5357-7430 | 4 | 8 |
7430-¥ | 7 | 8 |
Подсчитывая обычным способом статистику
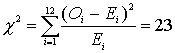
С вероятностью 0.95 значению
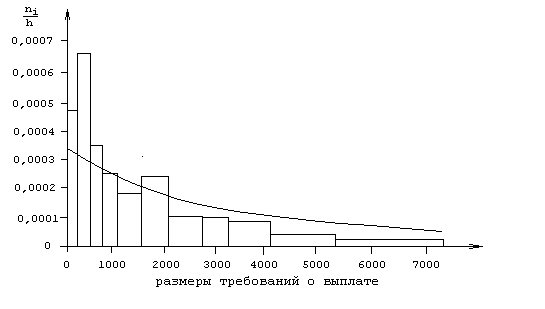
Рис 2.2. Гистограмма и подогнанная экспоненциальная модель
.Рисунок 2.2 показывает, что подгонка действительно плохая: требования размером около
£ 500 превышают подогнанные для них, а требования размером от £ 2000 до £ 7000, напротив, ниже подогнанных. Кроме того, очень большие требования превышают подогнанные (на гистограмме не отражено).Вывод таков: необходимо подобрать распределение, у которого бы “оба хвоста весили больше”, чем у экспоненциального распределения. Таким распределением может служить распределение Парето.
Для моделирования потерь страхования используется распределение Парето (см. п. 1.1.2.).
Напоминаем, что X~ P(a ,l ), если 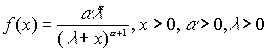 .
.
Оценим параметры распределения Парето, используя метод максимального правдоподобия. Пусть
Построим функцию правдоподобия
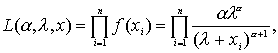
логарифм который выглядит следующим образом:
![]()
![]()
Найдем
![]()
откуда
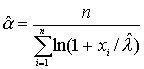 (2.1)
(2.1)
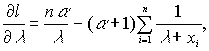
откуда
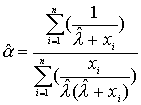 (2.2)
(2.2)
Приравнивая (2.1) и (2.2) получим уравнение для нахождения
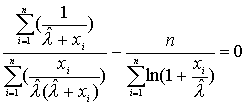
Это нелинейное уравнение, которое может быть решено с помощью численных методов. Однако необходимо знать начальное приближенное значение параметра l , которое можно получить применяя метод моментов для оценки параметров. Суть метода моментов заключается в том, что для параметров, которые известным образом составляются из моментов, оценку получают, заменяя моменты через эмпирические моменты.
Оценки параметров a и l распределения Парето с использованием метода моментов находятся из системы
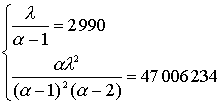
Откуда
Оценки по методу максимального правдоподобия можно получить, используя метод Ньютона:
Таким образом, имеются три подгонки под данные: первую дает экспоненциальная модель со средним 2980, вторая и третья являются моделями Парето, но с параметрами, найденными применением двух различных методов. Для сравнения подгонок используем критерий
Таблица 2.3. Зарегистрированные и ожидаемые величины для экспоненциальной модели и моделей Парето.
Класс | Зарегистриро- | Ожидаемые частоты | ||
ванные частоты | Экспоненциальная модель | Модель Парето | ||
Метод моментов | Метод максимального правдоподобия | |||
0-260 | 12 | 8 | 12,7 | 15,4 |
260-545 | 18 | 8 | 11,4 | 13,0 |
545-860 | 10 | 8 | 10,2 | 10,9 |
860-1212 | 8 | 8 | 9,1 | 9,3 |
1212-1612 | 7 | 8 | 8,2 | 8,0 |
1612-2073 | 10 | 8 | 7,4 | 6,9 |
2073-2618 | 5 | 8 | 6,7 | 6,0 |
2618-3285 | 6 | 8 | 6,1 | 5,3 |
3285-4145 | 6 | 8 | 5,6 | 4,8 |
4145-5357 | 3 | 8 | 5,2 | 4,4 |
5357-7430 | 4 | 8 | 5,1 | 4,2 |
7430-¥ | 7 | 8 | 8,3 | 7,7 |
Для каждого случая определим величину
Экспоненциальная модель:
Модель Парето (моменты):
Модель Парето (макс. правд.):
Очевидно, что модель Парето дает превосходную подгонку и существенно улучшает экспоненциальную модель. Между моделями Парето разница небольшая, хотя как и ожидалось подгонка методом максимального правдоподобия чуть лучше - с позиции критерия
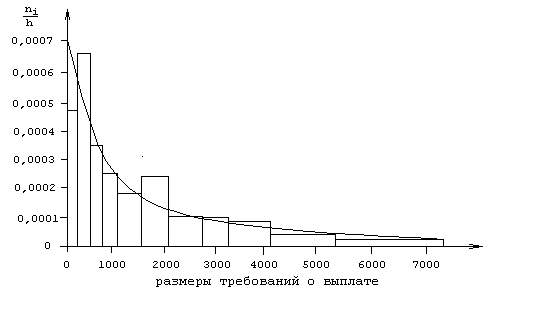
Рис 2.3. Гистограмма и подогнанная модель Парето (максимального правдоподобия).
Существует много других распределений “с тяжелым хвостом”, применяющихся для описания потерь страховщика: гамма-распределение, логнормальное, распределение Вейбулла и др.
Требование о выплате, предъявляемое страховой компании, должно быть оплачено в полном объеме, но, защищая себя от катастрофических выплат, компания может заключить договор страхования, который называется договором перестрахования. Рассмотрим договоры перестрахования двух типов: договор эксцедентного перестрахования и договор пропорционального перестрахования.
При пропорциональном перестраховании страховщик выплачивает оговоренную долю страховой выплаты, независимо от ее размера. Пропорциональное перестрахование можно описать так: если предъявлено требование о выплате X, то
Y=a X,
Z=(1-a )X
Параметр a называется долей удержания,
0<a <1; X - размер требования; Y - сумма, выплачиваемая страховщиком;Z - сумма, выплачиваемая перестраховщиком. Распределение выплат страховщика и перестраховщика может быть найдено простой заменой переменной.В ситуации эксцедентного перестрахования компания производит выплаты в полном объеме по всем требованиям, размеры которых не превосходят некоторой суммы M, называемой уровнем удержания; если размер требования превышает M, разница погашается перестраховщиком. Погашения эксцедентного договора перестрахования можно описать так: если поступает требование размером X, то компания платит сумму Y, где
Y=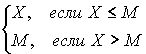
Перестраховщик платит сумму
Z, гдеZ=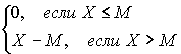
Очевидно,
X=Y+Z.Среднее значение страховой выплаты до заключения эксцендентного перестрахования
![]() ,
,
после заключения эксцендентного перестрахования
![]()
Величина, на которую уменьшается (в среднем) страховая выплата равна
![]()
Если под действием инфляции размеры требования о выплате
Xисчисляются как kX, где k - некоторый множитель, то среднее значение суммы, за которую отвечает страховщик имеет вид![]()
Типичные данные о частях страховых выплат, приходящихся на долю страховщика и зарегистрированные им, выглядят примерно так
x1,x2,M,x3,M,x4,x5,...
(2.3)Выборки вида (2.3) называются цензурованными. Цензурованные выборки получаются, когда некоторые величины регистрируются точно, а про оставшиеся известно только, что они превосходят определенную величину (например,
M).Для оценки параметров распределения, которому подчиняются страховые выплаты (в целом, с учетом частей страховщика и перестраховщика) используется метод максимального правдоподобия с функцией правдоподобия вида
![]()
где
F(X) - функция распределения страховых выплат;n - число страховых выплат, размеры которых xi - точно известны;
m - число страховых выплат, произведенных совместно с перестраховщиком.
Распределение страховых выплат перестраховщика.
Предположим, что распределение, которому подчиняются страховые выплаты, имеет плотность
f(x) и функцию F(x), перестраховщик располагает информацией лишь о выплатах, превосходящих M, т.е. Z = X-M, X ³ M. Функция плотности g(z) суммы Z, выплачиваемой перестраховщиком имеет вид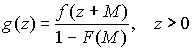 (2.4)
(2.4)
Договор страхования с безусловной франшизой предусматривает, что страхователь соглашается полностью принимать на себя ущерб, не превышающий некоторого предела L, который называется франшизой.
Если ущерб страхователя составляет сумму X, то страхователь может требовать только X-L, т.е. сумма Y, которую выплачивает по договору страховщик, равна
Y=
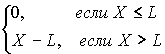
Если убытки по некоторому виду страхования описываются распределением с плотностью
f(x), тогда среднее страховой выплаты по договорам, предусматривающим безусловную франшизу L, составляет![]()
Между эксцедентным перестрахованием и безусловной франшизой существует тесная связь. Позиция страховщика заключившего договор с безусловной франшизой напоминает позицию перестраховщика, заключившего договор эксцедентного перестрахования.
Задачи
№ Пункта | Рекомендуемые задачи |
2.2 | 2.1 |
2.3 | 2.2, 2.3, 2.4 |
2.4.1 | 2.8 |
2.4.2 | 2.5, 2.6, 2.7, 2.9, 2.10 |
2.5 | 2.11, 2.12 |
2.1.
Предположим, что x1,x2,...,xn–независимые константы наблюдения, т.е. значения, которые принимала случайная величина Х, следующая экспоненциальному распределению с плотностью ![]() , q>0, x>0 .
, q>0, x>0 .
Найдите для q оценку максимального правдоподобия и определите асимптотическое распределение.
Подсказка: Примените теорему об оценках максимального правдоподобия (см. также задачи 1.10 и 1.11), реализовав следующие 3 этапа:
ЭТАП 1. Получите логарифм функции правдоподобия.
ЭТАП 2. Получите оценку максимального правдоподобия.
ЭТАП 3. Получите дисперсию асимптотического распределения.
2.2.
Пусть![]()
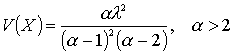
Подсказка: используйте интегрирование по частям.
2.3.
Используя метод моментов, найдите оценки параметров aи lраспределения Парето для данных из таблицы 2.1.2.4.
Пусть уровень собственного удержания компании составляет £25000. Используя распределение Парето, оцените вероятность того, что некоторое требование о выплате превзойдет указанный уровень.2.5.
Предположим, что Х следует экспоненциальному распределению со средним 1/l, M- уровень собственного удержания. Покажите, что сумма U имеет следующее среднее![]()
2.6.
Предположим, что распределение страховых выплат экспоненциальное со средним 1/l . Имеется n страховых выплат x1,x2,...,xn, зарегистрированных точно и m выплат, произведенных вместе с перестраховщиком, причем уровень собственного удержания равен M . Найдите для l оценку максимального правдоподобия, и укажите стандартную ошибку.2.7.
Пусть распределение страховых выплат (в целом) экспоненциальное со средним 1/l , и установлено собственное удержание M . Найдите распределение выплат, приходящихся на долю перестраховщика.2.8.
Пусть распределение потерь (общих) – экспоненциальное со средним 1/l , доля удержания равна a , любое требование о выплате погашается. Найдите распределение потерь: (a) страховщика, (b) перестраховщика.2.9.
Предположим, что страховые выплаты Х, производимые страховщиком, следуют распределению Парето. Покажите, что заключение договора перестрахования с уровнем удержания M приводит к тому, что среднее выплат, производимое страховщиком, уменьшается на![]()
2.10. Если распределение страховых выплат (в целом) является распределением ![]() и уровень собственного удержания равен M , покажите, что распределение выплат, производимых перестраховщиком, – это распределение
и уровень собственного удержания равен M , покажите, что распределение выплат, производимых перестраховщиком, – это распределение ![]()
Подсказка:
Используйте (2.4).2.11.
Убытки по некоторому страховому портфелю в течение первого года описываются распределением с плотностью f(x); действующая на втором году инфляция с показателем kобуславливает увеличение страховых выплат в k раз. Договор страхования предусматривает фиксированную безусловную франшизу. Покажите, что среднее страховых выплат, производимых в течение второго года, составляетE(Y)=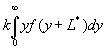
2.12.
В условиях предыдущей задачи предположите, что распределение убытков страхователей - это распределение Р(a,l). Покажите, что среднее страховых выплат на втором году таково:E(Y)=![]()
Подсказка:
одно решение вытекает из упражнение 2.11. (Можете ли Вы придумать еще одно?)