Глава
I. Материал по статистикеЕсли:
а) имеется
n независимых договоров страхования,б) вероятность требования одинакова для всех договоров и равна
p,то
число требований о выплате - N имеет биномиальное распределение с параметрами n и p (пишем N~ B(n,p)). Случайная величина Nпринимает значение r с вероятностью![]()
Если:
а) во время коротких временных интервалов Dt может быть предъявлено не более одного требования о выплате;
б) вероятность того, что будет предъявлено только одно требование о выплате равна lDt;
в) непересекающиеся временные интервалы независимы;
то число требований о выплате за период времени
t-N имеет распределение Пуассона с параметром lt (пишем N~ P(l t)). Случайная величина N принимает значение r с вероятностью![]()
где l - среднее значение числа требований о выплате за единичный период времени. Распределение Пуассона может использоваться в качестве хорошего приближения биномиального распределения, если
nвелико, а p мало. Тогда в качестве l нужно взять np.В обычном биномиальном распределении число испытаний n задано заранее, а значение вероятности случайной величины определяется числом неудач. В отрицательном биномиальном распределении значение вероятности случайной величины определяется числом независимых испытаний, при котором происходит фиксированное число неудач. Пусть k и r представляют соответственно число испытаний и фиксированное число неудач. Тогда плотность вероятности отрицательного биномиального распределения описывается выражением
![]()
Если
процесс предъявления требований о выплате является пуассоновским с показателем l
,то
случайная величина T - “период времени до первого требования о выплате” имеет функцию плотности экспоненциального распределения:f(t)=l e-l t
(пишемT~ E(l ))Нормальным называют распределение вероятностей непрерывной случайной величины
T, которое описывается плотностью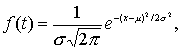
где m - математическое ожидание,
s- среднее квадратическое отклонение.
Пишем T~ N(m ,s2).
Соответствующая функция распределения имеет вид
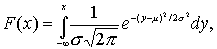
Вероятность попадания случайной величины
T в интервал (a ,b ) вычисляется по формуле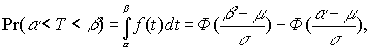
где Ф(
z) - функция Лапласа (Ф(z) - нечетная функция). Таблица значений функцииЗамечание. Нормальное распределение ограниченно используется для описания распределения размера требований выплат, поскольку последнее сильно несимметрично.
Случайная величина T имеет распределение Парето с параметром a и l , если
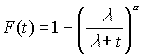
Распределение Парето имеет функцию плотности
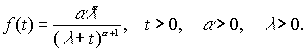
Пишем
T~ P(a ,l ).Случайная величина T имеет гамма-распределение с параметрами a и d , если
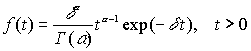
Функция Г(a ) - это известная гамма-функция, определяемая следующим образом
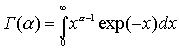
Пишем
T~ G(a ,d ).Взаимосвязь между различными распределениями вероятностей приведена в приложении 2.
Функцией распределения называют функцию
F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньше x, т.е.F(x)=P(X<x)
Свойства функции распределения
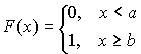
Первую производную от функции распределения
F(x) называют плотностью распределения вероятностей непрерывной случайной величины Xf(x)=F¢ (x)
Свойства плотности распределения
Математическое ожидание выступает как мера для среднего уровня требований о выплате.
Пусть
X - дискретная случайная величина, принимающая значения xi с вероятностью pi. Тогда математическое ожидание X - это величина![]()
Если
X~ B(n,p), то E(X)=np.Если
X~ P(l t), то E(X)=l t.Если
T - непрерывная случайная величина с функцией плотности f(t), t>0, то математическое ожидание задается следующим образом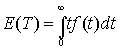
Если
T~ E(l ), то E(T)=1/l .Если
T~ N(m ,s2), то E(T)=m ..Если
T~ P(a ,l ), то E(T)=l /(a -1), a >1.Если
T~ G(a ,d ), то E(T)=a /d .Свойства математического ожидания
а)
E(a )=a , a =constб)
E(a X)=a E(X) , a =constв)
E(X1+X2)=E(X1)+E(X2)г)
E(X1X2)=E(X1)E(X2) , если X1,X2 - независимые случайные величины.Пример 1.1.
Имеется следующая информация по страховым выплатам, сделанным по 100 договорам автономного страхования
Число выплат | 0 | 1 | 2 |
Частота | 77 | 19 | 4 |
Найти среднее число выплат.
Решение.
Среднее число выплат определяется следующим образом
![]()
Условное математическое ожидание
Предполагаем, что число требований о выплате, сделанных по договору общего страхования -
N принимает значение ni с вероятностью pi. Пусть Xi - это размер i-го требования о выплате; предположим, что все Xi независимы друг от друга и от числа предъявляемых требований и имеют одно и то же математическое ожидание mx. Пусть T - общий размер требований о выплате. Тогда![]()
![]()
![]()
где m
N - математическое ожидание числа требований о выплате.Последний результат можно записать в форме
E(T)=EN(E(T|N))
(1.1)Пример 1.2.
В кошельке четыре монеты. Три из них ведут себя честно, т.е. вероятность выпадения орла при подбрасывании монеты равна -
Pr(орел)=0.5. Четвертая монета нечестная - Pr(орел)=0.8. Из кошелька вытаскивается одна монета и дважды подбрасывается. Каково математическое ожидание числа выпавших орлов?Решение.
Условное распределение числа выпавших орлов, при условии, что была вытащена “честная” монета - это распределение В(2;0.5), математическое ожидание которого равно 1; условное распределение числа орлов, при условии, что была вытащена “нечестная” монета - это распределение В(2;0.8) со средним значением, равным
1.6.Е(число орлов)=
Pr(монета “честная”)Е(число орлов|монета “честная”) + Pr(монета “нечестная”)Е(число орлов|монета “нечестная”) = 0.75*1 + 0.25*1.6. = 1.15.Дисперсия случайной величины X показывает колебания уровня требований около среднего значения, и определяется по формуле:
V(X)=E(X-E(X))2
Удобная формула для вычисления дисперсии:
V(X)=E(X2)-[E(X)]2
Если
X~ B(n,p)
, тоV(X)=npq, q=1-p;X~ P(l t),
тоV(X)=l t;X~ E(l ),
тоV(X)=1/l2;X~ N(a ,s2),
тоV(X)=s2;X~ P(a ,l ),
тоV(X)=al2/[(a -1)2(a -2)], a >2;X~ G(a ,d ),
тоV(X)=a /d2;Свойства дисперсии
а)
V(a )=0, a =constб)
V(a X)=a2V(X), a =constв)
V(X1+X2)=V(X1)+V(X2), если X1,X2 - независимые случайные величиныКогда желательно, чтобы оценка рассеивания имела размерность случайной величины, вычисляют среднее квадратическое отклонение
![]()
Аналогично формуле (1.1) условная дисперсия равна
V(T)=EN[V(T|N)]+VN[E(T|N)]
(1.2)Пример 1.3.
Вероятность предъявления требования о выплате по срочному договору страхования равна 0.1. Если требование о выплате имеет место, его размер следует равномерному распределению на интервале
[0,1000]. Найти среднее и дисперсию страховых выплат.Решение.
Пусть B~ U(0,1000)и I - индикатор требования о страховой выплате, т.е. I=0, если требование о выплате не предъявлено и I=1, если требование о выплате было предъявлено. Используя (1.1), (1.2) имеем
E(C) = EI [E(C|I)] = EI[E(B)I ]= E(B) E(I)=500 * 0.1 = 50
V(C) = EI[V(C|I)] + VI[E(C|I)] = EI[V(B)I] + VI[E(B)I] =
V(B) E(I) + E(B2) V(I) = (106 / 12) * 0.1 + 5002 * 0.1 * 0.9 = 30833
£ 50 при среднем квадратичном отклонении в £ 176.Часто применяемым средством для вычисления математических ожиданий является производящая функция моментов.
Момент порядка iслучайной величины X, обозначаемый через mi¢- это число, определяемое следующим образом
mi¢=E(Xi)
Здесь
E(X)= m1¢=m.Производящая функция моментов
(m.g.f.) случайной величины X определяется так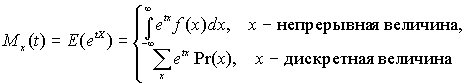
В случае, когда все моменты распределения существуют, можно выразить
Mx(t) в виде степенного ряда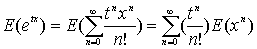
Отсюда сразу же получается выражение для момента
n-го порядка.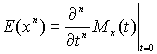
Пример 1.4.
Пусть
X~ B(n,p). Определить m.g.f.Решение.
![]()
![]()
По теореме Тейлора имеем
![]()
Пример 1.5.
Пусть
T~ E(l ). Найти m.g.f., E(T),V(T).Решение.
Имеем
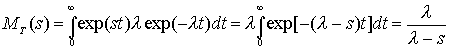
При вычислении интеграла был использован следующий трюк. Если
f(t), t>0 - это произвольная функция плотности, то![]()
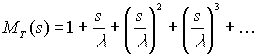
![]()
![]()
Пусть X1,X2,...,Xn - независимые и одинаково распределенные случайные величины. Предположим, что ![]() .
.
Центральная предельная теорема говорит о том, что случайная величина
![]()
имеет при больших
nраспределение, близкое к стандартному нормальному распределению, или в альтернативной формулировке![]()
Последнее приближение становится тем лучше, чем больше
n; другим фактором, влияющим на это является также асимметрия генеральной совокупности. Для генеральных совокупностей с симметричными плотностями приближение к нормальному распределению довольно близко уже для выборок с объемом по меньшей мере 10, в то время как для совокупностей, чьи плотности не симметричны, необходимый объем выборки должен быть 50 или даже больше.К несчастью, распределение размеров требований о выплате скорее сильно несимметрично, поэтому центральная предельная теорема применима здесь ограничено.
Пример 1.6.
Рассмотрим договор страхования жизни сроком на 10 лет. Вероятность предъявления требования о выплате по этому договору страхования равна 0.25. Предположим, что страховая компания заключила 100 независимых договоров страхования. Найти вероятность того, что к окончанию срока действия договора страхования (через 10 лет) будет предъявлено в точности 30 требований о выплате.
Решение.
Прежде чем мы начнем решать эту задачу, сделаем одно техническое замечание. Нормальное распределение непрерывно. Общее число требований о выплате -
X, которое будет предъявлено страховой компании, следует биномиальному распределению В(100, 0.25); это распределение дискретно. Таким образом, мы разыскиваем аппроксимацию (приближение) дискретного распределения с помощью непрерывного нормального распределения. В таких случаях мы мысленно заменяем значение 30, принимаемое дискретной случайной величиной X, следующей, биномиальному распределению, интервалом (29.5, 30.5), в котором принимает значение случайная величина Y, имеющая подходящее нормальное распределение. Используя математическое ожидание E(X)=npи дисперсию V(X)=npq биномиально распределенной случайной величины X, мы найдем, что аппроксимирующее нормальное распределение должно иметь следующие параметры:m = np = 100*0.25 = 25
s2 = npq = 100*0.25*0.75 = 18.75
По центральной предельной теореме
Pr(X = 30) » Pr(29.5 < Y < 30.5), где Y ~ N(25,18.75).
Вычислим последнюю вероятность, переходя к стандартному нормальному распределению. Используя таблицы для стандартного нормального распределения находим
Pr(29.5 < Y < 30.5) = Pr((29.5-25)/4.33 < Z < (30.5-25)/4.33) =
Pr(1.04 < Z < 1.27) = Ф(1.27) - Ф(1.04) = 0.898 - 0.851 = 0.047.
Точное вычисление
Pr(X = 30) дает 0.046.Пусть случайные величины X1,X2,...,Xn ассоциированы с некоторыми константами (наблюдениями) x1,x2,...,xn. Предположим, что все Xi независимы и имеют одну и ту же функцию плотности f(x,q ) (fзависит от q , т.е. от оценки; оценивается q0).
Для нахождения оценок максимального правдоподобия следует придерживаться такого алгоритма:
Метод максимального правдоподобия является довольно легким методом для получения оценок параметров статистических моделей, кроме того этот метод обеспечивает и вычисление дисперсии, эта дисперсия выглядит “лучше” дисперсий оценок, получаемых с помощью других методов.
Теорема об оценках максимального правдоподобия
Оценка
а) (приближенно) нормальное распределение;
б) математическое ожидание q
0;в) дисперсию
Пример 1.7.
Определенная часть портфеля автотранспортного страхования состоит из
n идентичных и независимых договоров страхования. Обозначим через xi число требований о выплате, предъявляемых (к данному моменту времени) по i-му договору страхования. Процесс предъявления требований о выплате пуассоновский с показателем l . Оценить параметр l.Решение.
Составляем функцию правдоподобия:
![]()
Логарифм функции правдоподобия выглядит следующим образом
![]()
где С - выражение, зависящее от фиксированных величин
xi и не зависящее от параметра l.Из условия
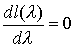 получаем
получаем 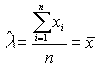
Вычислим дисперсию оценки
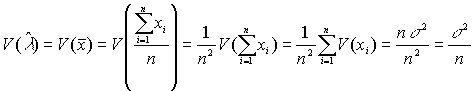 , где V(xi)=s2, i=1,...,n. Поскольку X~ P(l ) Þ V(x)=lÞ
, где V(xi)=s2, i=1,...,n. Поскольку X~ P(l ) Þ V(x)=lÞ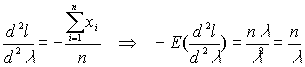
. ![]()
В основе байесовского метода лежит идея сопоставления неизвестному параметру некоторой случайной величины. Предполагается, что новый риск подчиняется априорному распределению. Теорема Байеса позволяет скорректировать априорное распределение, учитывая поступающую дополнительную информацию:
![]()
Здесь
f(q |данные) - апостериорное распределение;f(q ) - априорное распределение;
f(данные|q ) - функция правдоподобия.
Функция f(данные) не зависит отl, поэтому уравнение можно переписать так
f(q |данные)µ f(q )f(данные|q ),
где
µ- знак пропорциональности.Проблема заключается в выборе априорного распределения. Чаще всего пытаются выбирать априорное распределение в некотором достаточно обширном классе распределений, например, гамма-распределение.
Пример 1.8.
Пусть l~
G(a,d ), где![]()
Предположим, что страхователь предъявил за год
x требований о выплате и что x~ P(l ). Вычислим апостериорное распределение.Решение.
апост. плотность µ
апр. плотн. * плотн. макс. правд. =la-1exp(-dl ) * exp(-l )lxf(l |данные)µlx+a -1exp(-(d +1)l ), l >0
Из последнего соответствия видно, что апостериорная плотность является плотностью гамма - распределения
G(x+a ,d +1). Таким образом, как априорное, так и апостериорное распределение находятся в одном и том же классе распределений.При помощи критерия c2 проверяют, удовлетворяет ли рассматриваемая случайная величина X заданному закону распределения F0(x). Критерий согласия c2 служит для проверки гипотезы H0 о том, что FX(x)= F0(x), где FX(x) - функция распределения X, а F0(x) - заданное (гипотетическое) распределение.
Рассмотрим сначала случай, когда F0(x) не содержит неизвестных параметров. Область значений случайной величины Xделится на конечное число непересекающихся классов D1,...,Dk. При непрерывном X классы Di являются промежутками, при дискретном X - группами возможных значений X. Пусть pi - “теоретическая вероятность” того, что X попадает в Di, если гипотеза H0 верна. Если Di =[ai,bi], то pi=F0(bi)-F0(ai).
Теперь из
X производится выборка (X1,...,Xn) объема n. Пусть Mi - число значений выборки в Di. Тогда![]()
Разбиение на классы произвольно. Необходимо, однако, чтобы для граничных классов выполнялось неравенство
npi³1, для остальных классов npi³5; этого можно добиться за счет укрупнения классов. Если разбиение на классы удовлетворяет указанным требованиям, то контрольная величина равна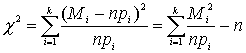
В предположении, что гипотеза
H0 верна, X имеет асимптотическое c2-распределение с m=k-1 степенями свободы. Так как c2 есть мера отклонения истинного распределения от гипотетического, то гипотеза отвергается, если значение, вычисленное по конкретной выборке согласно (1.4), превышает определенное критическое значение c2a, которое для заданного уровня значимости a и m=k-1 степеней свободы находится из таблицы 3 (см. приложение 3). Если c2³c2a, то гипотеза отвергается. Для n>30 значение c2aнаходятся уже не из таблицы, а вычисляются по формуле![]()
где
Z2a, определяемое равенством 2Ф0(Z2a)=1-2a, вычисляется по таблице 2 (см. приложение 2).Если гипотетическое распределение
F0(x) установлено неоднозначно, и гипотеза говорит лишь о том, что F0(x) относится к определенному множеству функций распределения F(x;q1,...,qr), которое зависит от r параметров. В этом случае поступают следующим образом: по выборке получают наиболее правдоподобные оценки параметровm=k-r-1 степеней свободы. В остальном критерий остается прежним.
Пример 1.9.
В портфеле автотранспортного страхования собрана информация о требованиях страховых выплат по 100000 годичных договоров страхования. В таблице показано зарегистрированное число страхователей, предъявивших 0,1,2,3,4,5 и более требований о выплате в течение года
Число требований | Число договоров |
0 | 81056 |
1 | 16174 |
2 | 2435 |
3 | 295 |
4 | 36 |
³ 5 | 4 |
Проверить, дает ли пуассоновская модель хорошее описание этих данных
?Решение.
Выберем для подгонки пуассоновскую модель с математическим ожиданием, совпадающим со средним значением приведенных данных. Предположим, что страхователи, предъявившие ³ 5 требований, предъявили на самом деле в точности 5 требований. Тогда
![]() .
.
По формуле
![]()
вычислим вероятность того, что по договору страхования будет предъявлено 0,1,2,... требований о выплате. Результаты расчетов приведем в таблице
Число требований | Вероятность |
0 | 0.801773 |
1 | 0.177136 |
2 | 0.019567 |
3 | 0.001440 |
4 | 0.000080 |
5 | 0.000004 |
Зарегистрированные и ожидаемые частоты требований о выплате представим в таблице
Число требований | Зарегистрированные частоты, Oi | Ожидаемые частоты, Ei |
0 | 81056 | 80177.3 |
1 | 16174 | 17713.6 |
2 | 2435 | 1956.7 |
3 | 295 | 144.0 |
4 | 36 | 8.0 |
³ 5 | 4 | 0.4 |
Итого | 100000 | 100000 |
Вычислим
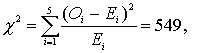
![]()
Вычислим c
2 с уровнем значимости 0.05 и числом степеней свободы 4.c2кр = c2(0.05;4)=9.5
Поскольку c
2кр > c2, то гипотеза об описании данных распределением Пуассона отвергается.Пусть X - дискретная случайная величина, принимающая значения 0,1,2,... с вероятностями p0,p1,p2,..... Производящая функция распределения определяется следующим образом
![]() (1.5)
(1.5)
Пример 1.10.
Предположим, что
X~ P(l ). Определить производящую функцию распределения.Решение.
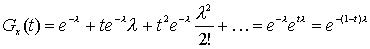 (1.6)
(1.6)
Производящая функция распределения:
Пусть, например,
X и Y- независимые и одинаково распределенные случайные величины с общей производящей функцией G(t), тогда![]()
Производящие функции обладают еще одним свойством - с их помощью можно вычислить моменты. По (1.5) имеем:
![]() (1.7)
(1.7)
Пусть случайная величина N описывает число требований о выплате, предъявляемых по некоторому договору общего страхования; случайные величины Xi соответствуют размерам требований о выплате. Рассмотрим модель процесса предъявления требований о выплате, согласно которой сначала выбирается число требований N, а потом независимо указывается размер каждого требования о выплате. Пусть T - общий размер требований о выплате. Тогда T имеет сложное распределение и
![]() (1.8)
(1.8)
где
Gx(t) - производящая функция распределения X,GN(t) -производящая функция распределения N.
Зная производящую функцию распределения легко получить моменты случайной величины
![]()
Задачи
№ Пункта | Рекомендуемые Задачи |
1.1.1. | 1.1 |
1.3.1. M | 1.2, 1.12, 1.16, 1.17, 1.25, 1.26 |
1.3.2. D | 1.3, 1.6 |
1.3.3. и.ф.м | 1.4, 1.5, 1.7 |
1.4. центр. пред. теор. | 1.8, 1.9 |
1.5.1. Оц. max правд. | 1.10, 1.11 |
1.5.2. Байесс. оц. | 1.13, 1.14 |
1.6. Пров. кач. подгонки | 1.15 |
1.7.1. Произв. ф-ции распр. | 1.18, 1.19, 1.20, 1.21 |
1.7.2. Сложн. распр. | 1.22, 1.23, 1.24 |
1.1.
Вероятность предъявления требования о выплате по 4 независимым договорам страхования жизни в календарном году равна 0.25. Найти вероятность того, что будет предъявлено 0,1,2,3,4 требования о страховой выплате. Определите вероятность того, что будет предъявлено 2 или более требований о выплате.1.2.
Вероятность предъявления требования о страховой выплате в связи со смертью по каждому из 4 договоров страхования жизни равна 0.25. Покажите, что математическое ожидание числа требований о выплате равно 1.Подсказка: Используйте задачу 1.1.
1.3.
Пусть X~ B(3,q). Покажите, что E(X2)=3q+6q2, V(X)=3pq.1.4.
Пусть X~ B(n,p). Используя m.g.f.. Используя формулу V(X) = E(X2) - E2(X), найдитеV(X).1.5.
Предположим, что Xимеет распределение Пуассона и математическое ожидание Xравно l . Покажите, что m.g.f. Xтакова, что![]() .
.
Выведите отсюда, что дисперсия
Xравна l (т.е. совпадает с математическим ожиданием).1.6.
Предположим, что Т~ Е(l). Покажите, что1.7.
ПустьX ~ N(m ,s2).Разложите m.g.f. в ряд по степеням t, и покажите, что E(X)=mи V(X)=s2.1.8.
Рассмотрим договор страхования жизни сроком на 10 лет. Вероятность предъявления требования о выплате по этому договору страхования равна 0.25. Предположим, что страховая компания заключила 100 независимых договоров страхования.Найдите вероятность того, что к окончанию срока действия договоров страхования будет предъявлено1.9.
Предположим, что число требований о выплате, предъявляемых по договорам автотранспортного страхования в течение календарного года следует распределению Пуассона с математическим ожиданием 0,2. Предположим, что имеется 100 идентичных и независимых договоров страхования, действующих на протяжении календарного года. Каково точное распределение общего числа требований о выплате, предъявленных за срок действия договора (за год)? Вычислите вероятность того, что будет предъявлено 19,20 и 21 требование о выплате на протяжение года. Какое нормальное распределение может использоваться для аппроксимации точного распределения? Почему в этом случае мы можем применять центральную предельную теорему? Каковы приближенные вероятности, что будет предъявлено 19,20 и 21 требование о выплате? Как сравнивать приближения с точными вероятностями?1.10.
Предположим, что размеры требований о выплате имеют экспоненциальное распределение Е(l ). Пусть x1,x2,...,xn-размеры требований о выплате, которые были предъявлены страховой компании. Покажите, что оценка максимального правдоподобия параметра l равна1.11.
Найдите аппроксимирующее распределение для оценки максимального правдоподобия из задачи 1.10.1.12.
Пусть X~ G(a ,d ). Покажите, что E(C)=1.13. Предположим, что мы располагаем данными о работе со страхователем, о котором говорилось в разделе 1.5.2, за n лет. Число требований о выплате, которые он предъявлял в каждые из этих n лет таково: x1,x2,...,xn. Покажите, что апостериорное распределение l-это распределение ![]() .
.
1.14. Используя задачи 1.12, 1.13,покажите, что математическое ожидание апостериорного распределения l после n лет имеет вид ![]() ;
;
покажите также, что последние выражение можно переписать так:
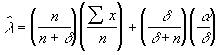
Что говорит это выражение об относительной значимости априорной информации
? Информации по договору страхования, накапливающейся с течением времени?1.15.
В течение некоторого срока велись записи о повреждениях (авариях) 2500 торговых кораблей определенного типа, застрахованных от повреждений (аварий) от избранного числа причин. Данные сгруппированы и приведены в таблице.Таблица частоты повреждений для
2500 торговых кораблейЧисло аварий( x) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ³ 7 |
Число кораблей с ( x) авариями | 1387 | 796 | 257 | 53 | 5 | 1 | 1 | 0 |
Подгоните эти данные пуассоновской модели и протестируйте ее, используя критерий c
2. (Покажите, что1.16.
Число требований о выплате по некоторому договору страхования за год-N,имеет распределение Пуассона с математическим ожиданием l . Требования о выплате независимо и с вероятностью р размер требования о выплате может принять некоторое большое значение (“большое” требование). Покажите, что математическое ожидание числа больших требований за год равно lp.1.17.
Годичное число автомобильных аварий без смертельного исхода на некотором перекрестке следует распределению Пуассона со средним 4,6. Число лиц в автомобиле(ях), попавших в какую-либо из этих аварий, может быть описано следующим образом:Число лиц в автомобиле(ях) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Вероятность | 0.1 | 0.3 | 0.1 | 0.1 | 0.1 | 0.1 | 0.05 | 0.05 | 0.05 | 0.05 |
Число рабочих дней, потерянных (вследствие травм, ушибов и т.д.) лицом, попавшим в одну из упомянутых аварий, может быть описано распределением Пуассона со средним 1,5. Найдите среднее значение общего числа рабочих дней, потерянных лицами, попавшими в течение года в аварии без смертельного исхода на указанном перекрестке.
1.18.
Предполагая, что Xимеет распределение B(n,p), покажите, что производящая функция X есть (1-p+pt)n.1.19. Предположим, что X~ P(l1), Y~ P(l2), причем X и Y независимы. Найдите производящую функцию X+Y, получите распределение X+Y.
1.20. Используя (1.6) и (1.7), проверьте, что математическое ожидание случайной величины, имеющей распределение P(l ) равно l.
1.21. Пусть X-случайная величина, принимающая целые значения, которая имеет производящую функцию G(t). Покажите, что
G¢¢ (t)=E(X2)-E(X),
и выведите отсюда равенство
V(X)=G¢¢ (1)+G¢ (1)-(G¢ (1))2.
Используя это равенство, вычислите дисперсию случайной величины с распределением
P(l ).1.22.
Пусть T - сумма случайного числа N величин Xi, Xi - независимы одинаково распределены. Покажите, что дисперсия Т может быть вычислена по формуле![]()
где
1.23. В условиях задачи 1.16 покажите, что число “больших” требований имеет распределение P(lp) . (Подсказка: используйте (1.8) и (1.6) и задачу 1.18.)
1.25.
Пусть Ii, i= 1,2,...,n - независимые случайные величины, такие, что Рr(Ii=1)= pи Рr(Ii = 0) = q = 1— р. Пусть X=а) Каково распределение
X ?b
) Покажите, что Е( Ii ) = р и V(Ii)=pq.с) Получите среднее и дисперсию биномиальной случайной величины.
1.26.
Вероятность предъявления требования о выплате по срочному договору страхования равна 0.05. Если требование о выплате имеет место, его размер подчиняется распределению Парето Р(3, 1000). Используя второй метод предыдущего примера, найдите среднее значение и среднее квадратическое отклонение размера требования о выплате.Подсказка: используйте упражнение
3.2.